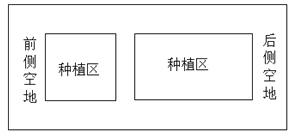
【题目】某村计划建造如图所示的矩形蔬菜温室,要求长宽的比为3:1,在温室内,沿前后两侧的内墙各留2.5m宽的空地放置工具,其他两侧内墙各留1m宽的通道.中间区域再留1m宽的通道,通道与前后墙平行,剩余空地(阴影部分)为种植区,当种植区面积是300m2,求矩形温室的长与宽是多少?
参考答案:
【答案】长为36m、宽为12m.
【解析】试题分析:首先设长为3xm,则宽为xm,然后根据题意列出关于x的一元二次方程,从而求出x的值,从而得出长和宽.
试题解析:解:设长为3xm,则宽为xm,根据题意列方程得:
(3x-6)(x-2)=300.
解之得:
x1=-8(舍去),x2=12m∴3x=36m
答:矩形温室的长为36m、宽为12m,种植区面积为300m2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,E是BC边的中点,连接DE并延长交AB的延长线于点F,则在题中条件下,下列结论不能成立的是( )
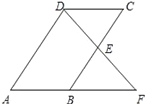
A. BE=CE B. AB=BF C. DE=BE D. AB=DC
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了落实党中央提出的“惠民政策”,我市今年计划开发建设A、B两种户型的“廉租房”共40套.投入资金不低于270万元,又不超过296万元.开发建设办公室预算:一套A型“廉租房”的造价为10万元,一套B型“廉租房”的造价为4.8万元.
(1)请问有几种开发建设方案?
(2) 在投入资金最少的方案下,为了让更多的人享受到“惠民”政策,开发建设办公室决定通过缩小“廉租房”的面积来降低造价、节省资金.每套A户型“廉租房”的造价降低1万元,每套B户型“廉租房”的造价降低0.3万元,将节省下来的资金全部用于再次开发建设缩小面积后的“廉租房”,如果同时建设A、B两种户型,请你直接写出再次开发建设的方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是半圆半径,半径OC⊥AB于点O,点D是弧BC的中点,连接CD、AD、OD,给出以下四个结论:①∠DOB=∠ADC;②CE=OE;③△ODE∽△ADO;④2CD2=CE·AB.其中正确结论的序号是( )

A. ①③ B. ②④ C. ①④ D. ①②③
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:我们知道
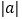 的几何意义是在数轴上数
的几何意义是在数轴上数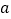 对应的点与原点的距离,即
对应的点与原点的距离,即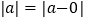 ,也就是说,
,也就是说,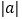 表示在数轴上数
表示在数轴上数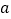 与数
与数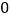 对应点之间的距离.这个结论可以推广为:
对应点之间的距离.这个结论可以推广为: 表示在数轴上数
表示在数轴上数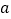 与
与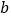 对应点之间的距离.
对应点之间的距离.例
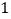 已知
已知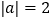 ,求
,求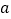 的值.
的值.解:在数轴上与原点距离为
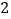 的点的对应数为
的点的对应数为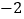 和
和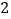 ,即
,即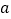 的值为
的值为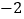 和
和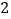 .
.例
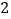 已知
已知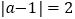 ,求
,求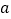 的值.
的值.解:在数轴上与
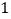 的距离为
的距离为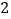 点的对应数为
点的对应数为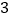 和
和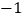 ,即
,即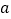 的值为
的值为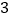 和
和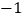 .
.仿照阅读材料的解法,解决下列问题:
(1)已知
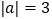 ,求
,求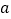 的值;
的值;(2)已知
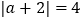 ,求
,求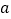 的值;
的值;(3)若数轴上表示
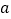 的点在
的点在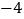 与
与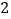 之间,则
之间,则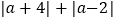 的值为_________;
的值为_________;(4)当
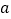 满足_________时,则
满足_________时,则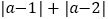 的值最小,最小值是_________.
的值最小,最小值是_________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O是坐标原点,菱形OABC的顶点A的坐标为
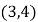 ,顶点C在x轴的正半轴上,则
,顶点C在x轴的正半轴上,则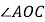 的角平分线所在直线的函数关系式为______.
的角平分线所在直线的函数关系式为______.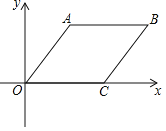
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=1,BC=2,点E在AD上,且ED=2AE.
(1)求证:△ABC∽△EAB.
(2)AC与BE交于点H,求HC的长.

相关试题

