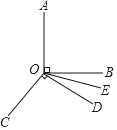
【题目】(10分)如图,已知∠AOB=90°,∠COD=90°,OE为∠BOD的平分线,∠BOE=17°18′,求∠AOC的度数.
参考答案:
【答案】145°24′.
【解析】试题分析:由OE是∠BOD的平分线,∠BOE=17°18′,可知∠EOD=∠BOE;又由∠COD=90°可得∠COB=90°-2∠BOE,又因为∠AOB=90°,所以∠AOC=90°-∠COB.
试题解析:∵OE为∠BOD的平分线,
∴2∠BOE=∠BOD,
∵∠BOE=17°18′,
∴∠BOD=34°36′,
∵∠AOB=∠COD=90°,∠AOB+∠COD+∠AOC+∠BOD=360°,
∴∠AOC=360°﹣∠AOB﹣∠COD﹣∠BOD=360°﹣90°﹣90°﹣34°36′=145°24′.
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD中,AD=BC,BE=DF,AE⊥BD,CF⊥BD,垂足分别为E,F.
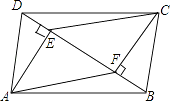
(1)求证:△ADE≌△CBF;
(2)若AC与BD相交于点O,求证:AO=CO. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(﹣1)4﹣|﹣3|×[2﹣(﹣3)2]
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=2x2﹣4x﹣2的对称轴是( )
A.直线x=﹣1B.直线x=1C.直线x=0D.直线y=1
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,△ABC中,∠ABC=45°,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点F.
求证:BF=AC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】命题“对顶角相等”的逆命题是命题(填“真”或“假”).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AC⊥BC,DE⊥AB,AD平分∠BAC,下面结论错误的是( )
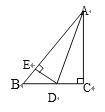
A.BD+ED=BC
B.DE平分∠ADB
C.AD平分∠EDC
D.ED+AC>AD
相关试题

