
【题目】某校“校园主持人大赛”结束后,将所有参赛选手的比赛成绩(得分均为整数)进行整理,并分别绘制成扇形统计图和频数直方图.部分信息如下:
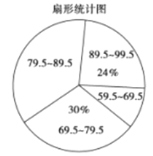
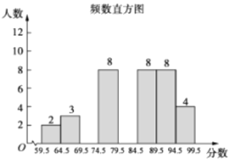
(1)本次比赛参赛选手共有________人,扇形统计图中“79.5~89.5”这一范围的人数占总参赛人数的百分比为________;
(2)补全图2频数直方图;
(3)赛前规定,成绩由高到低前40%的参赛选手获奖.某参赛选手的比赛成绩为88分,试判断他能否获奖,并说明理由;
(4)成绩前四名是2名男生和2名女生,若他们中任选2人作为该校文艺晚会的主持人,试求恰好选中1男1女为主持人的概率.
【答案】(1)50,36%;(2)见解析;(3)能获奖.理由见解析;(4)![]()
【解析】
(1)用“89.5~99.5”的人数和除以它们所占的百分比得到调查的总人数,再计算出“59.5~69.5”这两组所占的百分比,然后计算出“79.5~89.5”所占的百分比;
(2)根据“69.5~79.5”所占的百分比可求得“69.5~74.5”的人数,根据“79.5~89.5”所占的百分比可求得“79.5~84.5”的人数,从而补全统计图;
(3)计算出前40%有20人,恰好落在“84.5~99.5” 这一范围,从而可判断他能获奖;
(4)画树状图展示所有12种等可能的结果数,再找出恰好选中1男1女的结果数,然后根据概率公式求解.
(1)“89.5~99.5”的人数和它们所占的百分比分别是:(8+4)人和24%,
∴总人数为:![]() (人),
(人),
“59.5~69.5”的人数是5人,所占百分比是:![]() ,
,
∴“79.5~89.5”所占的百分比是:1-24%-10%-30%=36%,
故答案为:50,36%;
(2)∵“69.5~79.5” 的人数是:50![]() 30%=15(人),
30%=15(人),
∴“69.5~74.5”的人数是:15-8=7(人),
“79.5~89.5” 的人数是:50![]() 36%=18(人),
36%=18(人),
∴“79.5~84.5”的人数是:18-8=10(人),
补全条形图如图所示:
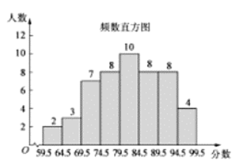
(3)能获奖.理由:
因为本次参赛选手共50人,所以前40%的人数为![]() (人)
(人)
由频数直方图可得84.5~99.5这一范围人数恰好![]() 人,
人,
又![]() ,所以能获奖;
,所以能获奖;
(4)画树状图为: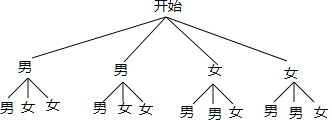
由树状图可知共有12种等可能的结果,恰好选中一男一女为主持人的结果有8种,
所以P(一男一女为主持人)![]() .
.
答:恰好选中一男一女为主持人的概率为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,AB是垂直于水平面的建筑物.为测量AB的高度,小红从建筑物底端B点出发,沿水平方向行走了5.2米到达点C,然后沿斜坡CD前进,到达坡顶D点处,DC=BC.在点D处放置测角仪,测角仪支架DE高度为0.8米,在E点处测得建筑物顶端A点的仰角∠AEF为27°(点A,B,C,D,E在同一平面内).斜坡CD的坡度(或坡比)i=1:2.4,求建筑物AB的高度.(参考数据sin27°≈0.45,cos27°≈0.89,tan27°≈0.51)

查看答案和解析>>
科目:初中数学 来源: 题型:
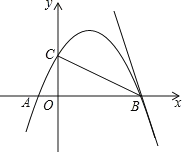
【题目】如图,抛物线y=ax2+bx+2经过点A(1,0),B(4,0),交y轴于点C;
(1)求抛物线的解析式(用一般式表示);
(2)点D为y轴右侧抛物线上一点,是否存在点D使S△ABC=![]() S△ABD?若存在,请求出点D坐标;若不存在,请说明理由;
S△ABD?若存在,请求出点D坐标;若不存在,请说明理由;
(3)将直线BC绕点B顺时针旋转45°,与抛物线交于另一点E,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E是边BC的中点,连接AE、DE,分别交BD、AC于点P、Q,过点P作PF⊥AE交CB的延长线于F,下列结论:
①∠AED+∠EAC+∠EDB=90°,
②AP=FP,
③AE=![]() AO,
AO,
④若四边形OPEQ的面积为4,则该正方形ABCD的面积为36,
⑤CEEF=EQDE.
其中正确的结论有( )

A.5个B.4个C.3个D.2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,D为AB边上的一点,以AD为直径的⊙O交BC于点E,交AC于点F,过点C作CG⊥AB交AB于点G,交AE于点H,过点E的弦EP交AB于点Q(EP不是直径),点Q为弦EP的中点,连结BP,BP恰好为⊙O的切线.
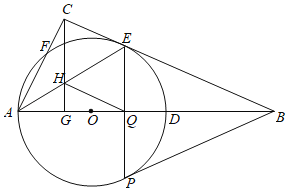
(1)求证:BC是⊙O的切线.
(2)求证:![]() =
=![]() .
.
(3)若sin∠ABC═![]() ,AC=15,求四边形CHQE的面积.
,AC=15,求四边形CHQE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边![]() 的边长为3,点
的边长为3,点![]() 在边
在边![]() 上,
上,![]() ,线段
,线段![]() 在边
在边![]() 上运动,
上运动,![]() ,有下列结论:
,有下列结论:
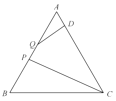
①![]() 与
与![]() 可能相等;②
可能相等;②![]() 与
与![]() 可能相似;③四边形
可能相似;③四边形![]() 面积的最大值为
面积的最大值为![]() ;④四边形
;④四边形![]() 周长的最小值为
周长的最小值为![]() .其中,正确结论的序号为( )
.其中,正确结论的序号为( )
A.①④B.②④C.①③D.②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,![]() 为坐标原点,直线
为坐标原点,直线![]() 交二次函数
交二次函数![]() 的图像于点
的图像于点![]() ,
,![]() ,点
,点![]() 在该二次函数的图像上,设过点
在该二次函数的图像上,设过点![]() (其中
(其中![]() )且平行于
)且平行于![]() 轴的直线交直线
轴的直线交直线![]() 于点
于点![]() ,交直线
,交直线![]() 于点
于点![]() ,以线段
,以线段![]() 、
、![]() 为邻边作矩形
为邻边作矩形![]() .
.

(1)若点![]() 的横坐标为8.
的横坐标为8.
①用含![]() 的代数式表示
的代数式表示![]() 的坐标;
的坐标;
②点![]() 能否落在该二次函数的图像上?若能,求出
能否落在该二次函数的图像上?若能,求出![]() 的值;若不能,请说明理由;
的值;若不能,请说明理由;
(2)当![]() 时,若点
时,若点![]() 恰好落在该二次函数的图像上,请直接写出此时满足条件的所有直线
恰好落在该二次函数的图像上,请直接写出此时满足条件的所有直线![]() 的函数表达式.
的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
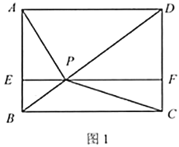
【题目】(1)如图1,点![]() 为矩形
为矩形![]() 对角线
对角线![]() 上一点,过点
上一点,过点![]() 作
作![]() ,分别交
,分别交![]() 、
、![]() 于点
于点![]() 、
、![]() .若
.若![]() ,
,![]() ,
,![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,则
,则![]() ________;
________;
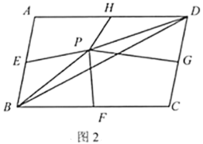
(2)如图2,点![]() 为
为![]() 内一点(点
内一点(点![]() 不在
不在![]() 上),点
上),点![]() 、
、![]() 、
、![]() 、
、![]() 分别为各边的中点.设四边形
分别为各边的中点.设四边形![]() 的面积为
的面积为![]() ,四边形
,四边形![]() 的面积为
的面积为![]() (其中
(其中![]() ),求
),求![]() 的面积(用含
的面积(用含![]() 、
、![]() 的代数式表示);
的代数式表示);
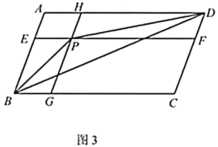
(3)如图3,点![]() 为
为![]() 内一点(点
内一点(点![]() 不在
不在![]() 上)过点
上)过点![]() 作
作![]() ,
,![]() ,与各边分别相交于点
,与各边分别相交于点![]() 、
、![]() 、
、![]() 、
、![]() .设四边形
.设四边形![]() 的面积为
的面积为![]() ,四边形
,四边形![]() 的面积为
的面积为![]() (其中
(其中![]() ),求
),求![]() 的面积(用含
的面积(用含![]() 、
、![]() 的代数式表示);
的代数式表示);
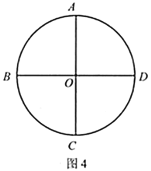
(4)如图4,点![]() 、
、![]() 、
、![]() 、
、![]() 把
把![]() 四等分.请你在圆内选一点
四等分.请你在圆内选一点![]() (点
(点![]() 不在
不在![]() 、
、![]() 上),设
上),设![]() 、
、![]() 、
、![]() 围成的封闭图形的面积为
围成的封闭图形的面积为![]() ,
,![]() 、
、![]() 、
、![]() 围成的封闭图形的面积为
围成的封闭图形的面积为![]() ,
,![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() .根据你选的点
.根据你选的点![]() 的位置,直接写出一个含有
的位置,直接写出一个含有![]() 、
、![]() 、
、![]() 、
、![]() 的等式(写出一种情况即可).
的等式(写出一种情况即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的布袋中装有三个小球,小球上分别标有数字![]() 、1、2,它们除了数字不同外,其它都完全相同.
、1、2,它们除了数字不同外,其它都完全相同.
(1)随机地从布袋中摸出一个小球,求摸出的球为标有数字1的小球的概率.
(2)小红先从布袋中随机摸出一个小球,记下数字作为![]() 的值,再把此球放回袋中搅匀,由小亮从布袋中随机摸出一个小球,记下数字作为
的值,再把此球放回袋中搅匀,由小亮从布袋中随机摸出一个小球,记下数字作为![]() 的值,请用树状图或表格列出
的值,请用树状图或表格列出![]() 、
、![]() 的所有可能的值,并求出直线
的所有可能的值,并求出直线![]() 不经过第四象限的概率.
不经过第四象限的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com