【题目】如图,在平面直角坐标系中,直线AB与x轴,y轴分别交于点A(﹣4,0),B(0,3),动点P从点O出发,沿x轴负方向以每秒1个单位的速度运动,同时动点Q从点B出发,沿射线BO方向以每秒2个单位的速度运动,过点P作PC⊥AB于点C,连接PQ,CQ,以PQ,CQ为邻边构造平行四边形PQCD,设点P运动的时间为t秒. 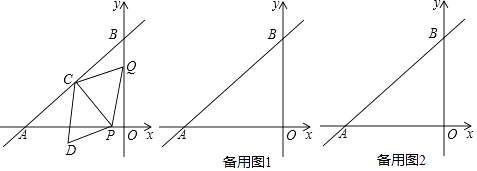
(1)当点Q在线段OB上时,用含t的代数式表示PC,AC的长;
(2)在运动过程中. ①当点D落在x轴上时,求出满足条件的t的值;
②若点D落在△ABO内部(不包括边界)时,直接写出t的取值范围;
(3)作点Q关于x轴的对称点Q′,连接CQ′,在运动过程中,是否存在某时刻使过A,P,C三点的圆与△CQQ′三边中的一条边相切?若存在,请求出t的值;若不存在,请说明理由.#D.
参考答案:
【答案】
(1)解:如图1中,
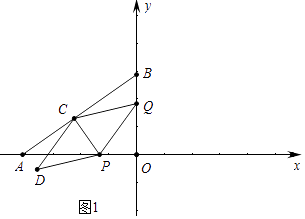
∵OA=3,OB=4,
∴AB= ![]() =
= ![]() =5,
=5,
在Rt△ACP中,PA=4﹣t,
∵sin∠OAB= ![]() =
= ![]() ,
,
∴PC= ![]() (4﹣t),
(4﹣t),
∵cos∠OAB= ![]() =
= ![]() ,
,
∴AC= ![]() (4﹣t)
(4﹣t)
(2)解:①当D在x轴上时,如图2中,

∵QC∥OA,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
解得t= ![]() .
.
∴t= ![]() s时,点D在x轴上,
s时,点D在x轴上,
②如图,

∵PQ∥AB,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴t= ![]() ,
,
综上所述,当 ![]() <t<
<t< ![]() 时,点D落在△ABO内部(不包括边界)
时,点D落在△ABO内部(不包括边界)
(3)解:如图3中,作QN⊥BC于N,
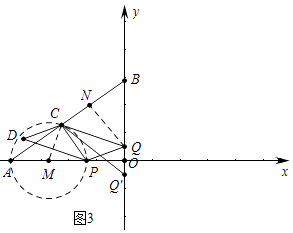
∵Q(0,3﹣2t),Q′(0,2t﹣3),
当QC与⊙M相切时,则QC⊥CM,
∴∠QCM=90°,∴∠QCP+∠PCM=90°,∵∠QCP+∠QCB=90°,
∴∠BCQ=∠PCM=∠CPM,
∵∠CPM+∠PAC=90°,∠OBA+∠OAB=90°,
∴∠APC=∠OBA,∴∠QBC=∠QCB,
∴BQ=CQ,
∵cos∠ABO= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
解得t= ![]() ,
,
当CQ′是⊙M切线时,同法可得 ![]() =
= ![]() ,
,
解得t= ![]() ,
,
∴t= ![]() s或
s或 ![]() 时,过A,P,C三点的圆与△CQQ′三边中的一条边相切
时,过A,P,C三点的圆与△CQQ′三边中的一条边相切
【解析】(1)利用三角函数sin∠OAB= ![]() =
= ![]() ,cos∠OAB=
,cos∠OAB= ![]() =
= ![]() ,列出关系式即可解决问题.(2)①当D在x轴上时,如图2中,由QC∥OA,得
,列出关系式即可解决问题.(2)①当D在x轴上时,如图2中,由QC∥OA,得 ![]() =
= ![]() ,由此即可解决问题.②当点D在AB上时,如图3中,由PQ∥AB,得
,由此即可解决问题.②当点D在AB上时,如图3中,由PQ∥AB,得 ![]() =
= ![]() ,求出时间t,求出①②两种情形时的△POQ的面积即可解决问题.(3)如图4中,当QC与⊙M相切时,则QC⊥CM,首先证明QB=QC,作QN∠BC于N,根据cos∠ABO=
,求出时间t,求出①②两种情形时的△POQ的面积即可解决问题.(3)如图4中,当QC与⊙M相切时,则QC⊥CM,首先证明QB=QC,作QN∠BC于N,根据cos∠ABO= ![]() =
= ![]() ,列出方程即可解决问题,当CQ′是⊙M切线时,方法类似.
,列出方程即可解决问题,当CQ′是⊙M切线时,方法类似.
-
科目: 来源: 题型:
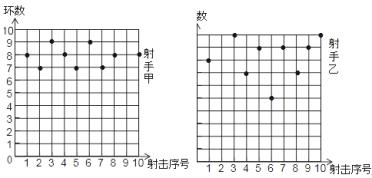
查看答案和解析>>【题目】甲、乙两名射手在相同条件下打靶,射中的环数如图所示,利用图中提供的信息,解答下列问题:
(1)分别求甲、乙两名射手中环数的众数和平均数;
(2)如果从甲、乙两名射手中选一名去参加射击比赛,你选谁去?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两名射击运动员在某次训练中各射击10发子弹,成绩如表:
甲
8
9
7
9
8
6
7
8
10
8
乙
6
7
9
7
9
10
8
7
7
10
且
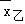 =8,S乙2=1.8,S甲2=1.2,根据上述信息完成下列问题:
=8,S乙2=1.8,S甲2=1.2,根据上述信息完成下列问题:(1)乙运动员射击训练成绩的众数是 ,中位数是 .
(2)求甲运动员射击成绩的平均数,并判断甲、乙两人在本次射击成绩的稳定性.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从背面相同的同一副扑克牌中取出红桃9张、黑桃10张、方块11张,现将这些牌洗匀背面朝上放在桌面上.
(1)求从中抽出一张牌是红桃的概率;
(2)现从桌面上先抽掉若干张黑桃,再放入与抽掉的黑桃张数相同的红桃,并洗匀且背面都朝上排开后,随机抽一张是红桃的概率不小于
 ,问至少抽掉了多少张黑桃?
,问至少抽掉了多少张黑桃?(3)若先从桌面上抽掉9张红桃和m(m>6)张黑桃后,再在桌面抽出一张牌.
①当m为何值时,事件“再抽出的这张牌是方块”为必然事件?
②当m为何值时,事件“再抽出的这张牌是方块”为随机事件?并求出这个事件的概率的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中表示下面各点:
A(0,3) B(1,-3) C(3,-5) D(-3,-5) E(3,5).连接CE,CD.
(1)A点到原点的距离是___个单位长度;B点到直线CD的距离是____个单位长度;
(2)将点C向x轴的负方向平移6个单位,它与点_______重合;
(3)直线CE与y轴的位置关系是_______;直线CE与x轴的位置关系是_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某中学举行“中国梦校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.

(1)根据图示填写下表;
平均数(分)
中位数(分)
众数(分)
初中部
85
高中部
85
100
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解学生参加体育活动的情况,学校对学生进行随机抽样调查,其中一个问题是“你平均每天参加体育活动的时间是多少”,共有4个选项:A 1.5小时以上;B 1~1.5小时;C 0.5~1小时;D 0.5小时以下.图1、2是根据调查结果绘制的两幅不完整的统计图,请你根据统计图提供的信息,解答以下问题:

(1)本次一共调查了多少名学生?
(2)在图1中将选项B的部分补充完整;
(3)若该校有3000名学生,你估计全校可能有多少名学生平均每天参加体育活动的时间在0.5小时以下.
相关试题

