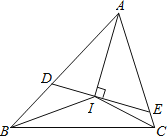
【题目】我们知道,任何一个三角形的三条内角平分线相交于一点,如图,若△ABC 的三条内角平分线相交于点I,过I作DE⊥AI分别交AB、AC于点D、E.

(1)请你通过画图、度量,填写右上表(图画在草稿纸上,并尽量画准确)
(2)从上表中你发现了∠BIC与∠BDI之间有何数量关系,请写出来,并说明其中的道理.

参考答案:
【答案】(1)∠BIC的度数110°;120°;135°;150°;∠BDI的度数110°;120°;135°;150°;(2)∠BIC=∠BDI
【解析】
试题分析:(1)通过画图、度量,即可完成表格;
(2)先从上表中发现∠BIC=∠BDI,再分别证明∠BIC=90°+![]() ∠BAC,∠BDI=90°+
∠BAC,∠BDI=90°+![]() ∠BAC.
∠BAC.
解:(1)填写表格如下:
∠BIC的度数110°;120°;135°;150°
∠BDI的度数110°;120°;135°;150°
(2)∠BIC=∠BDI,理由如下:
∵△ABC的三条内角平分线相交于点I,
∴∠BIC=180°﹣(∠IBC+∠ICB)
=180°﹣![]() (∠ABC+∠ACB)
(∠ABC+∠ACB)
=180°﹣![]() (180°﹣∠BAC)
(180°﹣∠BAC)
=90+![]() ∠BAC;
∠BAC;
∵AI平分∠BAC,
∴∠DAI=![]() ∠DAE.
∠DAE.
∵DE⊥AI于I,
∴∠AID=90°.
∴∠BDI=∠AID+∠DAI=90°+![]() ∠BAC.
∠BAC.
∴∠BIC=∠BDI.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某区新教师招聘中,七位评委独立给出分数,得到一列数.若去掉一个最高分和一个最低分,得到一列新数,那么这两列数的相关统计量中,一定相等的是 ( )
A. 中位数 B. 众数 C. 方差 D. 平均数
-
科目: 来源: 题型:
查看答案和解析>>【题目】六多边形的内角和为( )
A. 180° B. 360° C. 720° D. 1080°
-
科目: 来源: 题型:
查看答案和解析>>【题目】按下列要求,写出正确的不等式:
(1)由-2<-1,两边都加-a;
(2)由7>5,两边都乘以不为零的-a.
-
科目: 来源: 题型:
查看答案和解析>>【题目】写出命题“两直线平行,同位角相等”的结论部分:_____________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,把点P(3,2)绕原点O顺时针旋转90°,所得到的对应点P′的坐标为( )
A. (3,2) B. (2,﹣3) C. (﹣3,﹣2) D. (3,﹣2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b的图象与反比例函数y=
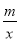 (x>0)的图象交于P(n,2),与x轴交于A(-4,0),与y轴交于点C,PB⊥x轴于点B,且AC=BC.
(x>0)的图象交于P(n,2),与x轴交于A(-4,0),与y轴交于点C,PB⊥x轴于点B,且AC=BC.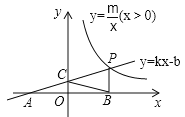
(1)求一次函数、反比例函数的解析式;
(2)反比例函数图象有一点D,使得以B,C,P,D为顶点的四边形是菱形,求出点D的坐标.
相关试题

