【题目】有一个如图示的长方体的透明玻璃杯,其长AD=8cm,高AB=6cm,水深为AE=4cm,在水面线EF上紧贴内壁G处有一粒食物,且EG=6cm,一小虫想从杯外的A处沿壁爬进杯内的G处吃掉食物.
(1)小虫应该走怎样的路线才使爬的路线最短呢?请你在图中画出它爬行的路线,并用箭头标注.
(2)求小虫爬行的最短路线长(不计杯壁厚度).

参考答案:
【答案】(1)作图见解析;(2)10cm.
【解析】试题分析:(1)作出A关于BC的对称点A′,连接A′G,与BC交于点Q,此时AQ+QG最短;
(2)A′G为直角△A′EG的斜边,根据勾股定理求解即可.
试题解析:(1)如图所示,AQ+QG为最短路程.

(2)∵在直角△AEG中,AE=4cm,AA′=12cm,
∴A′E=8cm,
又EG=6cm,
∴AQ+QG=A′Q+QG=A′G=![]() =10cm.
=10cm.
∴最短路线长为10cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰△ABC中,AD⊥BC于点D,且AD=
 BC,则△ABC底角的度数为( )
BC,则△ABC底角的度数为( )
A. 45° B. 75° C. 60° D. 45°或15°或75°
-
科目: 来源: 题型:
查看答案和解析>>【题目】一位同学拿了两块45°的三角尺△MNK、△ACB做了一个探究活动:将△MNK的直角顶点M放在△ABC的斜边AB的中点处,设AC=BC=a.
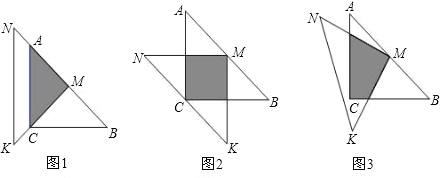
(1)如图1,两个三角尺的重叠部分为△ACM,则重叠部分的面积为 ,周长为 .
(2)将图1中的△MNK绕顶点M逆时针旋转45°,得到图2,此时重叠部分的面积为 ,周长为 .
2(3)如果将△MNK绕M旋转到不同于图1,图2的位置,如图3所示,猜想此时重叠部分的面积为多少?并试着加以验证.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知射线OC上的任意一点到∠AOB的两边的距离都相等,点D、E、F分别为边OC、OA、OB上,如果要想证得OE=OF,只需要添加以下四个条件中的某一个即可,请写出所有可能的条件的序号__________.
①∠ODE=∠ODF;②∠OED=∠OFD;③ED=FD;④EF⊥OC.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.(m2n)3=m5n3
B.a2a3=a6
C.(﹣y2)3=y6
D.﹣2x2+5x2=3x2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图:是长方形纸片ABCD折叠的情况,纸片的宽度AB=8cm,长AD=10cm,AD沿点A对折,点D正好落在BC上的M处,AE是折痕.
(1)求CM的长;
(2)求梯形ABCE的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ACD中,∠ADC=90°,AD=2,CD=1,点B在AD的延长线上,BD=l,连接BC.
(1)求BC的长;
(2)动点P从点A出发,向终点B运动,速度为1个单位/秒,运动时间为t秒.
①当t为何值时,△PDC≌△BDC;
②当t为何值时,△PBC是以PB为腰的等腰三角形?

相关试题

