【题目】如图,直线l1的解析表达式为:y=-3x+3,且l1与x轴交于点D,直线l2经过点A,B,直线l1,l2交于点C.
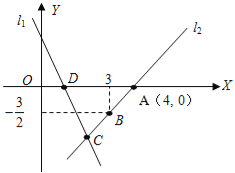
(1)求点D的坐标;
(2)求直线l2的解析表达式;
(3)求△ADC的面积;
(4)在直线l2上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,请直接写出点P的坐标.
参考答案:
【答案】(1)D(1,0);(2)![]() ;(3)
;(3)![]() ;(4)P(6,3).
;(4)P(6,3).
【解析】试题分析:(1)已知l1的解析式,令y=0求出x的值即可;
(2)设l2的解析式为y=kx+b,由图联立方程组求出k,b的值;
(3)联立方程组,求出交点C的坐标,继而可求出S△ADC;
(4)△ADP与△ADC底边都是AD,面积相等所以高相等,△ADC高就是点C到AD的距离.
解:(1)由y=﹣3x+3,令y=0,得﹣3x+3=0,
∴x=1,
∴D(1,0);
(2)设直线l2的解析表达式为y=kx+b,
由图象知:x=4,y=0;x=3,![]() ,代入表达式y=kx+b,
,代入表达式y=kx+b,
∴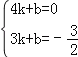 ,
,
∴ ,
,
∴直线l2的解析表达式为![]() ;
;
(3)由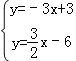 ,
,
解得![]() ,
,
∴C(2,﹣3),
∵AD=3,
∴S△ADC=![]() ×3×|﹣3|=
×3×|﹣3|=![]() ;
;
(4)△ADP与△ADC底边都是AD,面积相等所以高相等,△ADC高就是点C到直线AD的距离,即C纵坐标的绝对值=|﹣3|=3,
则P到AD距离=3,
∴P纵坐标的绝对值=3,点P不是点C,
∴点P纵坐标是3,
∵y=1.5x﹣6,y=3,
∴1.5x﹣6=3
x=6,
所以P(6,3).
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=x2﹣2x+4化为y=a(x﹣h)2+k的形式,下列正确的是( )
A. y=(x﹣1)2+2 B. y=(x﹣1)2+3
C. y=(x﹣2)2+2 D. y=(x﹣2)2+4
-
科目: 来源: 题型:
查看答案和解析>>【题目】25位同学10秒钟跳绳的成绩汇总如下表:
人数
1
2
3
4
5
10
次数
15
8
25
10
17
20
那么跳绳次数的中位数是_____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法不正确的有( )个
①从直线外一点到这条直线的垂线段,叫做点到直线的距离②内错角相等,③过一点有且只有一条直线与已知直线垂直④相等的角是对顶角
A. 0 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC=90°,D是边AC上的一点,连接BD,使∠A=2∠1,E是BC上的一点,以BE为直径的⊙O经过点D.
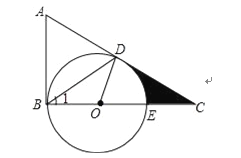
(1)求证:AC是⊙O的切线;
(2)若∠A=60°,⊙O的半径为2,求阴影部分的面积.(结果保留根号和π)
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分10分)从M地到N地有一条普通公路,总路程为120km;有一条高速公路,总路程为126km.甲车和乙车同时从M地开往N地,甲车全程走普通公路,乙车先行驶了另一段普通公路,然后再上高速公路.假设两车在普通公路和高速公路上分别保持匀速行驶,其中在普通公路上的行车速度为60km/h,在高速公路上的行车速度为100km/h.设两车出发x h时,距N地的路程为y km,图中的线段AB与折线ACD分别表示甲车与乙车的y与x之间的函数关系.
(1)填空:a= ,b= ;
(2)求线段AB、CD所表示的y与x之间的函数关系式;
(3)两车在何时间段内离N地的路程之差达到或超过30km?

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的个数是( )
①连接两点的线中,垂线段最短;
②两条直线相交,有且只有一个交点;
③若两条直线有两个公共点,则这两条直线重合;
④若AB+BC=AC,则A、B、C三点共线.
A. 2 B. 3 C. 4 D. 5
相关试题

