Question

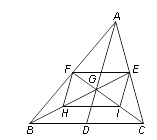
【题目】如图，△ABC的中线AD、BE、CF相交于点G，H、I分别是BG、CG的中点．

（1）求证：四边形EFHI是平行四边形；

（2）①当AD与BC满足条件 时，四边形EFHI是矩形；

②当AD与BC满足条件 时，四边形EFHI是菱形．

Answer 1

【答案】（1）证明见解析；（2）①AD⊥BC；②2AD=3BC

【解析】试题分析：（1）证出EF、HI分别是△ABC、△BCG的中位线，根据三角形中位线定理可得EF∥BC且EF=BC，HI∥BC且PQ=BC，进而可得EF∥HI且EF=HI．根据一组对边平行且相等的四边形是平行四边形可得结论；

（2）①由三角形中位线定理得出FH∥AD，再证出EF⊥FH即可；

②与三角形重心定理得出AG=AD，证出AG=BC，由三角形中位线定理和添加条件得出FH=EF，即可得出结论．

试题解析：（1）证明：∵BE，CF是△ABC的中线，∴EF是△ABC的中位线，∴EF∥BC且EF=BC．

∵H、I分别是BG、CG的中点．，∴HI是△BCG的中位线，∴HI∥BC且HI=BC，∴EF∥HI且EF=HI，∴四边形EFHI是平行四边形．

（2）解：①当AD与BC满足条件 AD⊥BC时，四边形EFHI是矩形；理由如下：

同（1）得：FH是△ABG的中位线，∴FH∥AG，FH=AG，∴FH∥AD，∵EF∥BC，AD⊥BC，∴EF⊥FH，∴∠EFH=90°，∵四边形EFHI是平行四边形，∴四边形EFHI是矩形；

故答案为：AD⊥BC；

②当AD与BC满足条件BC=AD时，四边形EFHI是菱形；理由如下：

∵△ABC的中线AD、BE、CF相交于点G，∴AG=AD，∵BC=AD，∴AG=BC，∵FH=AG，EF=BC，∴FH=EF，又∵四边形EFHI是平行四边形，∴四边形EFHI是菱形；

故答案为：2AD=3BC．