【题目】如图,在△ABC中,AB=AC,EF交AB于点E,交AC的延长线于点F,交BC于点D,且BE=CF.
求证:DE=DF.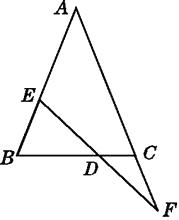
参考答案:
【答案】证明: 过点E作EG∥AC,交BC于点G ,  ,
,
∴∠F=∠DEG,∠ACB=∠EGB.
∵AB=AC,
∴∠ACB=∠B(等边对等角).
∴∠B=∠EGB.
∴BE=EG(等角对等边).
∵BE=CF,
∴EG=CF.
在△EGD和△FCD中,
∴△EGD≌△FCD(AAS).
∴DE=DF.
【解析】过点E作EG∥AC,交BC于点G , 根据二直线平行内错角,同位角相等得出∠F=∠DEG,∠ACB=∠EGB.根据等边对等角得出∠ACB=∠B,从而得出∠B=∠EGB.根据等角对等边得出BE=EG,从而得出EG=CF.然后利用AAS判断出△EGD≌△FCD,根据全等三角形对应边相等得出DE=DF。
-
科目: 来源: 题型:
查看答案和解析>>【题目】三角形两边的长分别是4和10,则此三角形第三边的长可能是( )
A. 16B. 11C. 6D. 5
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,D为BC边的中点,F为CA的延长线上的一点,过点F 作FG⊥BC于G点,并交AB于E点.
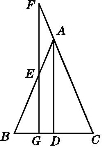
(1)求证:AD∥FG;
(2)△AFE为等腰三角形. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个角是40°,那么这个角的补角是______度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列函数关系中,属于正比例函数关系的是( )
A.圆的面积与它的半径
B.面积为常数S时矩形的长y与宽x
C.路程是常数时,行驶的速度v与时间t
D.三角形的底边是常数a时它的面积S与这条边上的高h -
科目: 来源: 题型:
查看答案和解析>>【题目】能把一个任意三角形分成面积相等的两部分的线段是三角形的( )
A. 角平分线 B. 中线 C. 高 D. 以上三种线
-
科目: 来源: 题型:
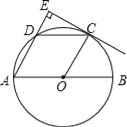
查看答案和解析>>【题目】如图,AB是⊙O的直径,点C、D为半圆O的三等分点,过点C作CE⊥AD,交AD的延长线于点E.
(1)求证:CE为⊙O的切线;
(2)判断四边形AOCD的形状,并说明理由.
相关试题

