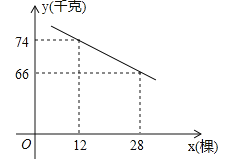
【题目】某片果园有果树80棵,现准备多种一些果树提高果园产量,但是如果多种树,那么树之间的距离和每棵树所受光照就会减少,单棵树的产量随之降低.若该果园每棵果树产果y(千克),增种果树x(棵),它们之间的函数关系如图所示.
(1)求y与x之间的函数关系式;
(2)在投入成本最低的情况下,增种果树多少棵时,果园可以收获果实6750千克?
(3)当增种果树多少棵时,果园的总产量w(千克)最大?最大产量是多少?
参考答案:
【答案】(1)y=﹣0.5x+80;(2)10;(3)当增种果树40棵时果园的最大产量是7200千克.
【解析】
试题分析:(1)函数的表达式为y=kx+b,把点(12,74),(28,66)代入解方程组即可.
(2)列出方程解方程组,再根据实际意义确定x的值.
(3)构建二次函数,利用二次函数性质解决问题.
试题解析:(1)设函数的表达式为y=kx+b,该一次函数过点(12,74),(28,66),得:![]() ,解得:
,解得:![]() ,∴该函数的表达式为y=﹣0.5x+80;
,∴该函数的表达式为y=﹣0.5x+80;
(2)根据题意,得,(﹣0.5x+80)(80+x)=6750,解得,![]() =10,
=10,![]() =70.
=70.
∵投入成本最低,∴![]() =70不满足题意,舍去,∴增种果树10棵时,果园可以收获果实6750千克.
=70不满足题意,舍去,∴增种果树10棵时,果园可以收获果实6750千克.
(3)根据题意,得:
w=(﹣0.5x+80)(80+x)=![]() ,∵a=﹣0.5<0,则抛物线开口向下,函数有最大值,∴当x=40时,w最大值为7200千克,∴当增种果树40棵时果园的最大产量是7200千克.
,∵a=﹣0.5<0,则抛物线开口向下,函数有最大值,∴当x=40时,w最大值为7200千克,∴当增种果树40棵时果园的最大产量是7200千克.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若记y=f(x)=
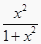 ,其中f(1)表示当x=1时y的值,即f(1)=
,其中f(1)表示当x=1时y的值,即f(1)= 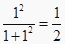 ;f(
;f( 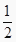 )表示当x=
)表示当x= 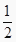 时y的值,即
时y的值,即 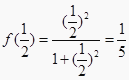 ;…;则f(1)+f(2)+f(
;…;则f(1)+f(2)+f( 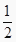 )+f(3)+f(
)+f(3)+f( 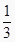 )+…+f(2011)+f(
)+…+f(2011)+f( 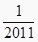 )=。
)=。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(
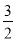 ,0),B(0,2),则点B2016的坐标为 .
,0),B(0,2),则点B2016的坐标为 .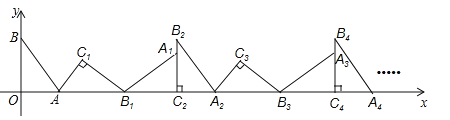
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,将二次函数
 的图象M沿x轴翻折,把所得到的图象向右平移2个单位长度后再向上平移8个单位长度,得到二次函数图象N.
的图象M沿x轴翻折,把所得到的图象向右平移2个单位长度后再向上平移8个单位长度,得到二次函数图象N.(1)求N的函数表达式;
(2)设点P(m,n)是以点C(1,4)为圆心、1为半径的圆上一动点,二次函数的图象M与x轴相交于两点A、B,求
 的最大值;
的最大值;(3)若一个点的横坐标与纵坐标均为整数,则该点称为整点.求M与N所围成封闭图形内(包括边界)整点的个数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某网店尝试用单价随天数而变化的销售模式销售一种商品,利用30天的时间销售一种成本为10元/件的商品售后,经过统计得到此商品单价在第x天(x为正整数)销售的相关信息,如表所示:

(1)请计算第几天该商品单价为25元/件?
(2)求网店销售该商品30天里所获利润y(元)关于x(天)的函数关系式;
(3)这30天中第几天获得的利润最大?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店有两个进价不同的计算器都卖了64元,其中一个盈利60%,另一个亏损20%,在这次买卖中,这家商店( )
A.不赔不赚
B.赚了32元
C.赔了8元
D.赚了8元 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A、O、B三点在同一条直线上,OD平分∠AOC,OE平分∠BOC.
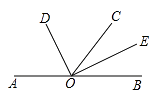
(1)若∠BOC=62°,求∠DOE的度数;
(2)若∠BOC=a°,求∠DOE的度数;
(3)图中是否有互余的角?若有请写出所有互余的角.
相关试题

