【题目】如图,AB是⊙O的直径,弦CD⊥AB,∠C=30°,CD=2 ![]() ,则阴影部分的面积为
,则阴影部分的面积为 
参考答案:
【答案】![]()
【解析】解:如图,连接OD,假设线段CD、AB交于点E,
∵AB是⊙O的直径,弦CD⊥AB,
∴CE=ED= ![]() ,
,
又∵∠DCB=30°,
∴∠DOE=2∠CDB=60°,∠ODE=30°,
∴OE=DEcot60°= ![]() ×
× ![]() =1,OD=2OE=2,
=1,OD=2OE=2,
∴S阴影=S扇形ODB﹣S△DOE+S△BEC= ![]() ﹣
﹣ ![]() OE×ED+
OE×ED+ ![]() BEEC=
BEEC= ![]() ﹣
﹣ ![]() +
+ ![]() =
= ![]() .
.
所以答案是: ![]() .
.
【考点精析】利用垂径定理和扇形面积计算公式对题目进行判断即可得到答案,需要熟知垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】将矩形纸片OABC放在平面直角坐标系中,0为坐标原点,点A在y轴上,点C在x轴上,点B的坐标是(8,6),点P是边AB上的一个动点,将△OAP沿OP折叠,使点A落在点Q处.
(1)如图①,当点Q恰好落在OB上时.求点p的坐标;
(2)如图②,当点P是AB中点时,直线OQ交BC于M点.
①求证:MB=MQ;②求点Q的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=ax+|a-1|的图象经过点(0,2),且函数y的值随x的增大而减小,则a的值为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用配方法解一元二次方程x2-6x-1=0时,方程可变形为( )
A. (x-3)2=10 B. (x-6)2=37 C. (x-3)2=4 D. (x-3)2=1
-
科目: 来源: 题型:
查看答案和解析>>【题目】某茶叶厂用甲,乙,丙三台包装机分装质量为200g的茶叶,从它们各自分装的茶叶中分别随机抽取了20盒,得到它们的实际质量的方差如下表所示:
甲包装机
乙包装机
丙包装机
方差
10.96
5.96
12.32
根据表中数据,可以认为三台包装机中,包装茶叶的质量最稳定是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x=1是一元二次方程x2+kx-3=0的一个根,则k的值为( )
A. -2 B. 2 C. 4 D. -4
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校的科技节比赛设置了如下项目:A—船模;B—航模;C—汽模.右图为该校参加科技比赛的学生人数统计图.
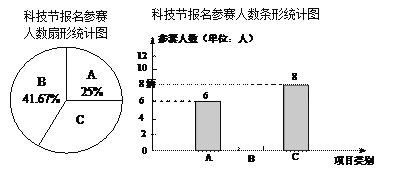
(1)该校报名参加B项目学生人数是 人;
(2)该校报名参加C项目学生人数所在扇形的圆心角的度数是 °;
(3)为确定参加区科技节的学生人选,该校在集训后进行了校内选拔赛,最后一轮复赛,决定在甲、乙2名候选人中选出1人代表学校参加区科技节B项目的比赛,每人进行了4次试飞,对照一定的标准,判分如下:甲:80,70,100,50;乙:75,80,75,70.如果你是教练,你打算安排谁代表学校参赛?请说明理由.
相关试题

