Question

【题目】（10分）如图（1）在ΔABC中，∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN于点D，BE⊥MN于点E．

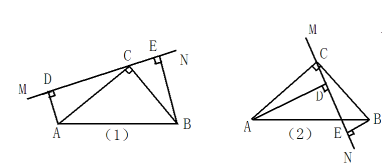
（1）求证：①ΔADC≌ΔCEB ②DE=AD+BE

（2）当直线MN绕点C旋转到图（2）的位置时，DE、AD、BE 有怎样的关系？并加以证明．

Answer 1

【答案】详见解析．

【解析】

试题分析：（1）由∠ACB＝90°，得∠ACD+∠BCE=90°，而AD⊥MN于D，BE⊥MN于点E，则∠ADC=∠CEB=90°，根据等角的余角相等得到∠ACD=∠CBE，易得△ADC≌△CEB，所以AD=CE，DC=BE，即可得到DE=DC+CE=BE+AD．（2）根据等角的余角相等得到∠ACD=∠CBE，易得△ADC≌△CEB，得到AD=CE，DC=BE，所以DE=CE-CD=AD-BE．

试题解析：（1）证明：∵∠ACB＝90°，

∴∠ACD+∠BCE=90°，

而AD⊥MN于D，BE⊥MN于点E，

∴∠ADC=∠CEB=90°，

∴∠ACD+∠BCE=90°∠BCE+∠CBE=90°，

∴∠ACD=∠CBE．

在△ADC和△CEB中，

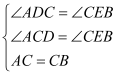
∴△ADC≌△CEB，

∴AD=CE，DC=BE，

∴DE=DC+CE=BE+AD；

DE=AD-BE；理由如下：

在△ADC和△CEB中，

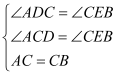
∴△ADC≌△CEB，

∴AD=CE，DC=BE，

∴DE =CE-CD=AD-BE；