【题目】已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC与点E、F,垂足为O.

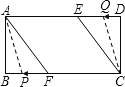
(1)如图1,连接AF、CE.求证四边形AFCE为菱形,并求AF的长;
(2)如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周,即点P自A→F→B→A停止,点Q自C→D→E→C停止,在运动过程中,已知点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒,当A、C、P、Q四点为顶点的四边形是平行四边形时,求t的值.
参考答案:
【答案】(1)AF=5cm;(2)t=![]() .
.
【解析】
试题分析:(1)根据全等推出OE=OF,得出平行四边形AFCE,根据菱形判定推出即可,根据菱形性质得出AF=CF,根据勾股定理得出方程,求出方程的解即可;
(2)分情况讨论可知,当P点在BF上、Q点在ED上时,才能构成平行四边形,根据平行四边形的性质列出方程求解即可.
(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠EAO=∠FCO,
∵AC的垂直平分线EF,
∴OA=OC,
在△AOE和△COF中,
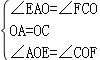 ,
,
∴△AOE≌△COF(ASA),
∴OE=OF,
∵OA=OC,
∴四边形AFCE是平行四边形,
∵EF⊥AC,
∴四边形AFCE是菱形.
∴AF=FC,
设AF=xcm,
则CF=xcm,BF=(8﹣x)cm,
∵四边形ABCD是矩形,
∴∠B=90°,
∴在Rt△ABF中,
由勾股定理得:42+(8﹣x)2=x2,
解得x=5,即AF=5cm;
(2)显然当P点在AF上时,Q点在CD上,此时A、C、P、Q四点不可能构成平行四边形;
同理P点在AB上时,Q点在DE或CE上或P在BF,Q在CD时不构成平行四边形,也不能构成平行四边形.
因此只有当P点在BF上、Q点在ED上时,才能构成平行四边形,
∴以A、C、P、Q四点为顶点的四边形是平行四边形时,PC=QA,
∵点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒,
∴PC=5t,QA=12﹣4t,
∴5t=12﹣4t,
解得t=![]() .
.
∴以A、C、P、Q四点为顶点的四边形是平行四边形时,t=![]() 秒.
秒.
-
科目: 来源: 题型:
查看答案和解析>>【题目】 (2016湖南湘西州第14题)一个等腰三角形一边长为4cm,另一边长为5cm,那么这个等腰三角形的周长是( )
A.13cm B.14cm C.13cm或14cm D.以上都不对
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x2﹣6x﹣5=0配方可变形为( )
A.(x+3)2=14
B.(x﹣3)2=4
C.(x﹣3)2=14
D.(x+3)2=4 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个数中,是正数的是( )
A. -(-1) B. -|-1| C. +(-1) D. (-1)3
-
科目: 来源: 题型:
查看答案和解析>>【题目】金泉街道改建工程指挥部,要对某路段工程进行招标,接到了甲、乙两个工程队的投标书.从投标书中得知:甲队单独完成这项工程所需天数是乙队单独完成这项工程所需天数的
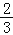 ;若由甲队先做10天,剩下的工程再由甲、乙两队合作30天可以完成.
;若由甲队先做10天,剩下的工程再由甲、乙两队合作30天可以完成.(1)求甲、乙两队单独完成这项工程各需要多少天?
(2)已知甲队每天的施工费用为0.84万元,乙队每天的施工费用为0.56万元,工程预算的施工费用为50万元.为缩短工期以减少对住户的影响,拟安排甲、乙两队合作完成这项工程,则工程预算的施工费用是否够用?若不够用,需追加预算多少万元?请给出你的判断并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,直线
 ⊥
⊥ 于点
于点 ,△
,△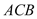 是直角三角形,且∠
是直角三角形,且∠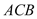 =90°,斜边
=90°,斜边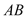 交直线
交直线 于点
于点 ,
, 平分∠
平分∠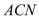 ,∠
,∠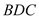 的平分线交
的平分线交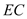 的延长线于点
的延长线于点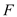 ,∠
,∠ =36°.
=36°.(1)如图1,当
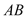 ∥
∥ 时,求∠
时,求∠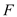 的度数.
的度数.(2)如图2,当△
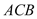 绕
绕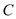 点旋转一定的角度(即
点旋转一定的角度(即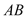 与
与 不平行),其他条件不变,问∠
不平行),其他条件不变,问∠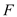 的度数是否发生改变?请说明理由.
的度数是否发生改变?请说明理由.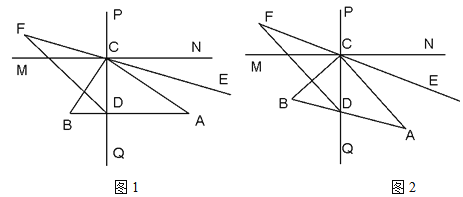
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列方程,属于一元一次方程的是( )
A. 2x-(1-x) B. x-xy=0 C. 2y2+y-1=0 D. x=0
相关试题

