[题目]∠1 与∠2 互为邻补角.∠1=36°.∠2= . 题目和参考答案 ——青夏教育精英家教网—

【题目】∠1 与∠2 互为邻补角，∠1=36°，∠2=_____.

参考答案：

【答案】144°

【解析】

两个角有一条公共边，它们的另一条边互为反向延长线，具有这种关系的两个角叫做邻补角；进而可得互为邻补角的两个角组成了一个平角，再结合平角的定义得到∠1+∠2=180°，即可求出∠2的度数.

若∠1与∠2互为邻补角，则∠1+∠2=180°.

∵∠1=36°，

∴∠2=144°.

故答案为144°.

相关试题

科目： 来源： 题型：

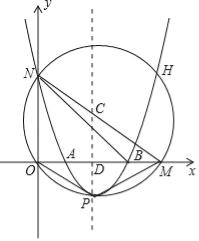
【题目】如图所示，在平面直角坐标系中，⊙C经过坐标原点O，且与x轴，y轴分别相交于M（4，0），N（0，3）两点．已知抛物线开口向上，与⊙C交于N，H，P三点，P为抛物线的顶点，抛物线的对称轴经过点C且垂直x轴于点D．
（1）求线段CD的长及顶点P的坐标；
（2）求抛物线的函数表达式；
（3）设抛物线交x轴于A，B两点，在抛物线上是否存在点Q，使得S四边形OPMN=8S△QAB，且△QAB∽△OBN成立？若存在，请求出Q点的坐标；若不存在，请说明理由．
查看答案和解析>>
科目： 来源： 题型：

【题目】阅读材料：
在平面直角坐标系xOy中，点P（x0，y0）到直线Ax+By+C=0的距离公式为：d=．
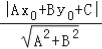例如：求点P0（0，0）到直线4x+3y﹣3=0的距离．
解：由直线4x+3y﹣3=0知，A=4，B=3，C=﹣3，
∴点P0（0，0）到直线4x+3y﹣3=0的距离为d==．
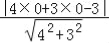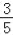根据以上材料，解决下列问题：
问题1：点P1（3，4）到直线y=﹣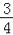x+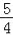的距离为；
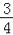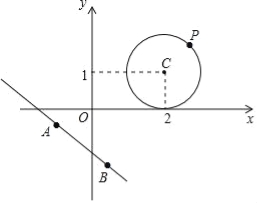
问题2：已知：⊙C是以点C（2，1）为圆心，1为半径的圆，⊙C与直线y=﹣x+b相切，求实数b的值；
问题3：如图，设点P为问题2中⊙C上的任意一点，点A，B为直线3x+4y+5=0上的两点，且AB=2，请求出S△ABP的最大值和最小值．
查看答案和解析>>
科目： 来源： 题型：

【题目】坐标系中，点 P（－3,4）到 y 轴的距离是_____.
查看答案和解析>>
科目： 来源： 题型：

【题目】计算
（1）5a﹣11a+7a
（2）3（x﹣2y）﹣4（2y﹣x）+x﹣2y
查看答案和解析>>
科目： 来源： 题型：

【题目】某市为创建全国文明城市，开展“美化绿化城市”活动，计划经过若干年使城区绿化总面积新增360万平方米．自2013年初开始实施后，实际每年绿化面积是原计划的1.6倍，这样可提前4年完成任务．
（1）问实际每年绿化面积多少万平方米？
（2）为加大创城力度，市政府决定从2016年起加快绿化速度，要求不超过2年完成，那么实际平均每年绿化面积至少还要增加多少万平方米？
查看答案和解析>>
科目： 来源： 题型：

【题目】若n是一个两位正整数，且n的个位数字大于十位数字，则称n为“两位递增数”（如13，35，56等）．在某次数学趣味活动中，每位参加者需从由数字1，2，3，4，5，6构成的所有的“两位递增数”中随机抽取1个数，且只能抽取一次．
（1）写出所有个位数字是5的“两位递增数”；
（2）请用列表法或树状图，求抽取的“两位递增数”的个位数字与十位数字之积能被10整除的概率．
查看答案和解析>>