【题目】如图，△ABC中，D是BC上的一点，若AB=10，BD=6，AD=8，AC=17，求△ABC的面积．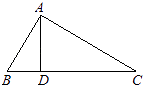

参考答案：

【答案】解：∵BD2+AD2=62+82=102=AB2 ， ∴△ABD是直角三角形，
∴AD⊥BC，
在Rt△ACD中， ，
∴S△ABC= ，
因此△ABC的面积为84．
答：△ABC的面积是84
【解析】根据AB=10，BD=6，AD=8，利用勾股定理的逆定理求证△ABD是直角三角形，再利用勾股定理求出CD的长，然后利用三角形面积公式即可得出答案．
【考点精析】利用勾股定理的概念和勾股定理的逆定理对题目进行判断即可得到答案，需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；如果三角形的三边长a、b、c有下面关系：a2+b2=c2，那么这个三角形是直角三角形．

关闭