【题目】如图,在矩形OABC中,OA=3,OC=5,分别以OA、OC所在直线为x轴、y轴,建立平面直角坐标系,D是边CB上的一个动点(不与C、B重合),反比例函数y=![]() (k>0)的图象经过点D且与边BA交于点E,连接DE.
(k>0)的图象经过点D且与边BA交于点E,连接DE.
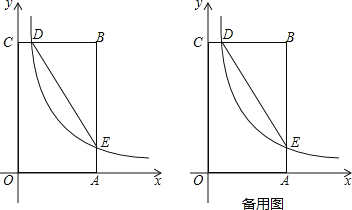
(1)连接OE,若△EOA的面积为2,则k= ;
(2)连接CA、DE与CA是否平行?请说明理由;
(3)是否存在点D,使得点B关于DE的对称点在OC上?若存在,求出点D的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)k=4.(2)平行,理由见解析;(3)满足条件的点D存在,D的坐标为D(0.96,5).
【解析】
试题分析:(1)连接OE,根据反比例函数k的几何意义,即可求出k的值;
(2)连接AC,设D(x,5),E(3,![]() ),则BD=3﹣x,BE=5﹣
),则BD=3﹣x,BE=5﹣![]() ,得到
,得到![]() ,从而求出
,从而求出
DE∥AC.
(3)假设存在点D满足条件.设D(x,5),E(3,![]() ),则CD=x,BD=3﹣x,BE=5﹣
),则CD=x,BD=3﹣x,BE=5﹣![]() ,AE=
,AE=![]() .作EF⊥OC,垂足为F,易得,△B′CD∽△EFB′,然后根据对称性求出B′E、B′D的表达式,列出
.作EF⊥OC,垂足为F,易得,△B′CD∽△EFB′,然后根据对称性求出B′E、B′D的表达式,列出![]() ,即
,即![]() =
=![]() ,从而求出(5﹣
,从而求出(5﹣![]() )2+x2=(3﹣x)2,即可求出x值,从而得到D点坐标.
)2+x2=(3﹣x)2,即可求出x值,从而得到D点坐标.
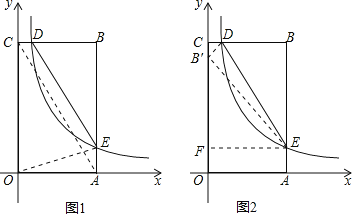
解:(1)连接OE,如,图1,
∵Rt△AOE的面积为2,
∴k=2×2=4.
(2)连接AC,如图1,设D(x,5),E(3,![]() ),则BD=3﹣x,BE=5﹣
),则BD=3﹣x,BE=5﹣![]() ,
,
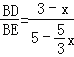 =
=![]() ,
,![]()
∴![]()
∴DE∥AC.
(3)假设存在点D满足条件.设D(x,5),E(3,![]() ),则CD=x,
),则CD=x,
BD=3﹣x,BE=5﹣![]() ,AE=
,AE=![]() .
.
作EF⊥OC,垂足为F,如图2,
易证△B′CD∽△EFB′,
∴![]() ,即
,即![]() =
=![]() ,
,
∴B′F=![]() ,
,
∴OB′=B′F+OF=B′F+AE=![]() +
+![]() =
=![]() ,
,
∴CB′=OC﹣OB′=5﹣![]() ,
,
在Rt△B′CD中,CB′=5﹣![]() ,CD=x,B′D=BD=3﹣x,
,CD=x,B′D=BD=3﹣x,
由勾股定理得,CB′2+CD2=B′D2,
(5﹣![]() )2+x2=(3﹣x)2,
)2+x2=(3﹣x)2,
解这个方程得,x1=1.5(舍去),x2=0.96,
∴满足条件的点D存在,D的坐标为D(0.96,5).
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列结论正确的是( )
A.若a2=b2 , 则a=b
B.若a>b,则a2>b2
C.若a,b不全为零,则a2+b2>0
D.若a≠b,则a2≠b2 -
科目: 来源: 题型:
查看答案和解析>>【题目】定义一种新运算“⊕”:a⊕b=a﹣2b,比如:2⊕(﹣3)=2﹣2×(﹣3)=2+6=8.
(1)求(﹣3)⊕2的值;
(2)若(x﹣3)⊕(x+1)=1,求x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某地6月1日至6月7日每天最高、最低气温的折线统计图。
请你根据折线统计图,回答下列问题:
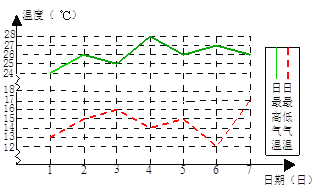
(1)在这7天中,日温差最大的一天是6月_____日;
(2)求这7天的日最高气温的平均数;
(3)求这7天日最高气温的方差。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知三角形三边长分别为a、b、c,其中a、b满足(a﹣6)2+|b﹣8|=0,求这个三角形最长边c的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将0.00025用科学计数法表示为( )
A. 2.5×104 B. 0.25×10-4 C. 2.5×10-4 D. 25×10-5
-
科目: 来源: 题型:
查看答案和解析>>【题目】正五边形的外角和等于 (度).
相关试题

