【题目】对于平面直角坐标系xOy中的点P(a,b),若点P′的坐标为(![]() ,ka+b)(其中k为常数,且k≠0),则称点P′为点P的“k属派生点”.
,ka+b)(其中k为常数,且k≠0),则称点P′为点P的“k属派生点”.
例如:P(1,4)的“2属派生点”为P′(1+![]() ,2×1+4),即P′(3,6).
,2×1+4),即P′(3,6).
(1)①点P(﹣1,﹣2)的“2属派生点”P′的坐标为 _________ ;
②若点P的“k属派生点”P′的坐标为(3,3),请写出一个符合条件的点P的坐标_________ ;
(2)若点P在x轴的正半轴上,点P的“k属派生点”为P′点,且△OPP′为等腰直角三角形,求k的值.
参考答案:
【答案】(1)(﹣2,﹣4);(1,2)(2)±1
【解析】
试题分析:(1)①只需把a=﹣1,b=﹣2,k=2代入(![]() ,ka+b)即可求出P′的坐标.
,ka+b)即可求出P′的坐标.
②由P′(3,3)可求出k=1,从而有a+b=3.任取一个a就可求出对应的b,从而得到符合条件的点P的一个坐标.
(2)设点P坐标为(a,0),从而有P′(a,ka),显然PP′⊥OP,由条件可得OP=PP′,从而求出k.
试题解析:(1)①当a=﹣1,b=﹣2,k=2时,
∴![]() =﹣1+
=﹣1+![]() =﹣2,ka+b=2×(﹣1)﹣2=﹣4.
=﹣2,ka+b=2×(﹣1)﹣2=﹣4.
∴点P(﹣1,﹣2)的“2属派生点”P′的坐标为(﹣2,﹣4).
故答案为:(﹣2,﹣4).
②由题可得: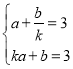 ,
,
∴ka+b=3k=3.
∴k=1.
∴a+b=3.
∴b=3﹣a.
当a=1时,b=2,此时点P的坐标为(1,2).
故答案为:(1,2).
说明:只要点P的横坐标与纵坐标的和等于3即可.
(2)∵点P在x轴的正半轴上,
∴b=0,a>0.
∴点P的坐标为(a,0),点P′的坐标为(a,ka).
∴PP′⊥OP.
∵△OPP′为等腰直角三角形,
∴OP=PP′.
∴a=±ka.
∵a>0,
∴k=±1.
故答案为:±1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程3(x-7)-5(x-4)=35,下列去括号正确的是( )
A. 3x-7-5x-4=35
B. 3x-21-5x-4=35
C. 3x-21-5x-20=35
D. 3x-21-5x+20=35
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P(2019,-2020)所在的象限是( )
A. 第一象限B. 第二象限C. 第三象限D. 第四象限
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O中,FG、AC是直径,AB是弦,FG⊥AB,垂足为点P,过点C的直线交AB的延长线于点D,交GF的延长线于点E,已知AB=4,⊙O的半径为
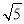 .
.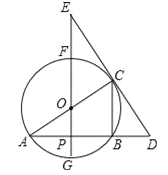
(1)分别求出线段AP、CB的长;
(2)如果OE=5,求证:AP=BP=
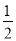 AB=2;
AB=2;(3)如果tan∠E=
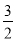 ,求DE的长.
,求DE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】点P向上平移1个单位长度后,再向左平移2个单位长度得到对应点Q(-1,3),则P点坐标是( )
A. (0,1) B. (-3,4) C. (2,1) D. (1,2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】“校园手机”现象越来越受到社会的关注﹒春节期间,小明随机调查了城区若干名同学和家长对中学生带手机现象的看法.统计整理并制作了如下的统计图:
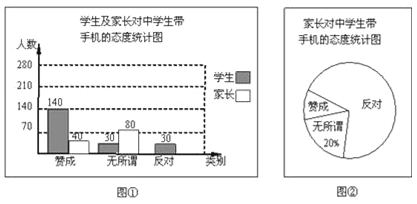
(1)这次的调查对象中,家长有 人;
(2)图②中表示家长“赞成”的圆心角的度数为 度;
(3)开学后,甲、乙两所学校对各自学校所有学生带手机情况进行了统计,发现两校共有2384名学生带手机,且乙学校带手机的学生数是甲学校带手机学生数的
 ,求甲、乙两校中带手机的学生数各有多少?
,求甲、乙两校中带手机的学生数各有多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,A(﹣2,2),B(﹣3,﹣2).
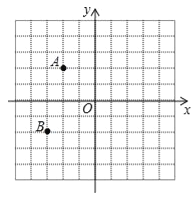
(1)①若点C与点A关于原点O对称,则点C的坐标为 ;②将点A向右平移5个单位得到点D,则点D的坐标为 ;
(2)在由点A,B,C,D组成的四边形ABCD内(不包括边界)任取一个横、纵坐标均为整数的点,求所取的点恰好落在双曲线
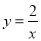 的概率.
的概率.
相关试题

