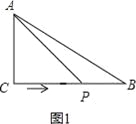
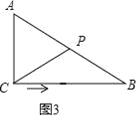
【题目】如图,在△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点C出发,按C→B→A的路径,以2cm每秒的速度运动,设运动时间为t秒,当t为___________时,△ACP是等腰三角形.

参考答案:
【答案】3s
【解析】试题分析:根据题意分四种情况,针对每种情况画出相应的图形,求出相应的时间t的值即可解答本题.第一种情况:当AC=CP时,△ACP是等腰三角形,如图1所示,∵在△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点C出发,按C→B→A的路径,以2cm每秒的速度运动,∴CP=6cm,∴t=6÷2=3秒;第二种情况:当CP=PA时,△ACP是等腰三角形,如图2所示,∵在△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点C出发,按C→B→A的路径,以2cm每秒的速度运动,∴AB=10cm,∠PAC=∠PCA,∴∠PCB=∠PBC,∴PA=PC=PB=5cm,∴t=(CB+BP)÷2=(8+5)÷2=6.5秒;第三种情况:当AC=AP时,△ACP是等腰三角形,如图3所示,∵在△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点C出发,按C→B→A的路径,以2cm每秒的速度运动,∴AP=6cm,AB=10cm,∴t=(CB+BA﹣AP)÷2=(8+10﹣6)÷2=6秒;第四种情况:当AC=CP时,△ACP是等腰三角形,如图4所示,作CD⊥AB于点D,∵∠ACB=90°,AC=6cm,BC=8cm,tan∠A=![]() ,∴
,∴![]() ,AB=10cm,设CD=4a,则AD=3a,∴(4a)2+(3a)2=62,解得,a=
,AB=10cm,设CD=4a,则AD=3a,∴(4a)2+(3a)2=62,解得,a=![]() ,∴AD=3a=
,∴AD=3a=![]() ,∴t=
,∴t=![]() =7.2s.
=7.2s.
故答案为:3,6或6.5或7.2.


-
科目: 来源: 题型:
查看答案和解析>>【题目】若方程(m2-1)x2-mx-x+2=0是关于x的一元一次方程,则代数式|m-1|的值为( )
A. 0 B. 2 C. 0或2 D. -2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,D为△ABC的边AB的延长线上一点,过D作DF⊥AC,垂足为F,交BC于E,且BD=BE,求证:△ABC是等腰三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式2x﹣2≤7的正整数解分别是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】中国是世界上13个贫水国家之一.某校有800名在校学生,学校为鼓励学生节约用水,展开“珍惜水资源,节约每一滴水”系列教育活动,为响应学校号召,数学小组做了如下调查:
小亮为了解一个拧不紧的水龙头的滴水情况,记录了滴水时间和烧杯中的水面高度,如图1.小明设计了调查问卷,在学校随机抽取一部分学生进行了问卷调查,并制作出统计图.如图2和图3.结合图2和图3回答下列问题:

(1)参加问卷调查的学生人数为 60 人,其中选C的人数占调查人数的百分比为 .
(2)在这所学校中选“比较注意,偶尔水龙头滴水”的大概有 人.若在该校随机抽取一名学生,这名学生选B的概率为 .
请结合图1解答下列问题:
(3)在“水龙头滴水情况”图中,水龙头滴水量(毫升)与时间(分)可以用我们学过的哪种函数表示?请求出函数关系式 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(3a2-2a+1)-(2a2+3a-5)的结果是( )
A. a2-5a+6 B. 7a2-5a-4 C. a2+a-4 D. a2+a+6
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个两位数,十位数字是a,个位数字是b,则这个两位数可以表示为( )
A. ab B. 10a+b C. 10b+a D. a+b
相关试题

