【题目】已知二次函数y=x2﹣4x+3.
(1)把这个二次函数化成y=a(x﹣h)2+k的形式;
(2)写出二次函数的对称轴和顶点坐标;
(3)求二次函数与x轴的交点坐标;
(4)画出这个二次函数的图象;
(5)观察图象并写出y随x增大而减小时自变量x的取值范围.
(6)观察图象并写出当x为何值时,y>0.
参考答案:
【答案】(1)y=(x﹣2)2﹣1;(2)对称轴是直线x=2,顶点坐标为(2,﹣1);(3)(1,0)(3,0);(4)见解析;(5)当y随x增大而减小时x≤2;(6)当x<1或x>3时,y>0.
【解析】
试题分析:(1)利用配方法先提出二次项系数,再加上一次项系数的一半的平方来凑完全平方式,把一般式转化为顶点式.
(2)根据(1)中的二次函数解析式直接写出答案;
(3)将已知函数解析式转化为两点式方程即可得到答案;
(4)根据顶点坐标,抛物线与y轴的交点坐标以及抛物线与x轴的交点坐标画出图象;
(5)(6)根据图象写出x的取值范围.
解:(1)y=x2﹣4x+3=(x﹣2)2﹣1,则该抛物线解析式是y=(x﹣2)2﹣1;
(2)由(1)知,该抛物线解析式为:y=(x﹣2)2﹣1,
所以对称轴是直线x=2,顶点坐标为(2,﹣1);
(3)∵二次函数y=x2﹣4x+3=(x﹣1)(x﹣3),
∴二次函数与x轴的交点坐标分别是:(1,0)(3,0);
(4)其图象如图所示:
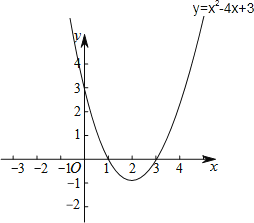
(5)由图象知,当y随x增大而减小时x≤2;
(6)由图象知,当x<1或x>3时,y>0.
-
科目: 来源: 题型:
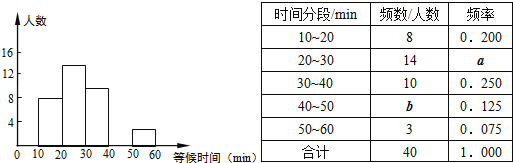
查看答案和解析>>【题目】某公园元旦期间,前往参观的人非常多.这期间某一天某一时段,随机调查了部分入园游客,统计了他们进园前等候检票的时间,并绘制成如下图表.表中“10~20”表示等候检票的时间大于或等于10min而小于20min,其它类同.
(1)这里采用的调查方式是 (填“普查”或“抽样调查”),样本容量是 ;
(2)表中a= ,b= ,并请补全频数分布直方图;
(3)在调查人数里,若将时间分段内的人数绘成扇形统计图,则“40~50”的圆心角的度数是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于平面图形上的任意两点P,Q,如果经过某种变换得到新图形上的对应点P′,Q′,保持PQ=P′Q′,我们把这种变换称为“等距变换”,下列变换中不一定是等距变换的是( )
A.平移 B.旋转 C.轴对称 D.位似
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据下面给出的数轴,解答下面的问题:
(1)请你根据图中A,B两点的位置,分别写出它们所表示的有理数.
(2)请问A,B两点之间的距离是多少?
(3)在数轴上画出与点A的距离为2的点(用不同于A,B的其它字母表示),并写出这些点表示的数.
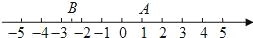
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个等腰三角形的两边长分别为2和4,则该等腰三角形的周长是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,AB=AC,∠A=36°,两条角平分线BE、CD相交于点O,则图中等腰三角形有( )
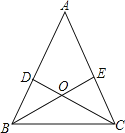
A.3个 B.5个 C.7个 D.8个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a﹣7b=﹣2,则﹣2a+14b+4的值是( )
A.0 B. 2 C.4 D.8
相关试题

