【题目】根据要求回答问题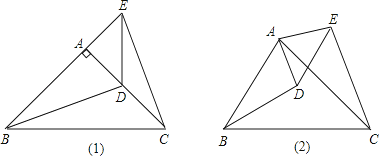
(1)如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=90°.
①当点D在AC上时,如图1,线段BD、CE有怎样的数量关系和位置关系?直接写出你猜想的结论;
②将图1中的△ADE绕点A顺时针旋转α角(0°<α<90°),如图2,线段BD、CE有怎样的数量关系和位置关系?请说明理由.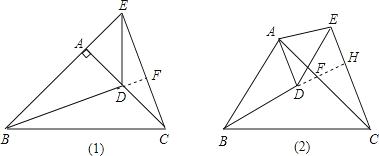
(2)当△ABC和△ADE满足下面甲、乙、丙中的哪个条件时,使线段BD、CE在(1)中的位置关系仍然成立?不必说明理由.
甲:AB:AC=AD:AE=1,∠BAC=∠DAE≠90°;
乙:AB:AC=AD:AE≠1,∠BAC=∠DAE=90°;
丙:AB:AC=AD:AE≠1,∠BAC=∠DAE≠90°.
参考答案:
【答案】
(1)
解:①结论:BD=CE,BD⊥CE;
②结论:BD=CE,BD⊥CE…1分
理由如下:∵∠BAC=∠DAE=90°
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,即∠BAD=∠CAE…1分
在△ABD与△ACE中,
∵ 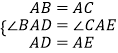
∴△ABD≌△ACE(SAS)
∴BD=CE
延长BD交AC于F,交CE于H.
在△ABF与△HCF中,
∵∠ABF=∠HCF,∠AFB=∠HFC
∴∠CHF=∠BAF=90°
∴BD⊥CE
(2)
解:结论:乙.AB:AC=AD:AE,∠BAC=∠DAE=90°
【解析】(1)①BD=CE,BD⊥CE.根据全等三角形的判定定理SAS推知△ABD≌△ACE,然后由全等三角形的对应边相等证得BD=CE、对应角相等∠ABF=∠ECA;然后在△ABD和△CDF中,由三角形内角和定理可以求得∠CFD=90°,即BD⊥CF;
②BD=CE,BD⊥CE.根据全等三角形的判定定理SAS推知△ABD≌△ACE,然后由全等三角形的对应边相等证得BD=CE、对应角相等∠ABF=∠ECA;作辅助线(延长BD交AC于F,交CE于H)BH构建对顶角∠ABF=∠HCF,再根据三角形内角和定理证得∠BHC=90°;(2)根据结论①、②的证明过程知,∠BAC=∠DFC(或∠FHC=90°)时,该结论成立了,所以本条件中的∠BAC=∠DAE≠90°不合适.
-
科目: 来源: 题型:
查看答案和解析>>【题目】东方红中学位于东西方向的一条路上,一天我们学校的李老师出校门去家访,他先向西走100米到聪聪家,再向东走150米到青青家,再向西走200米到刚刚家,请问:
(1)如果把这条路看作一条数轴,以向东为正方向,以校门口为原点,请你在这条数轴上标出聪聪家与青青家的大概位置(数轴上一格表示50米).
(2)聪聪家与刚刚家相距多远?
(3)聪聪家向西20米所表示的数是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在纸面上有一数轴(如图),折叠纸面.
(1)若表示﹣1的点与表示3的点重合,回答以下问题:
①表示5的点与表示数_________的点重合;
②若数轴上A、B两点之间的距离为9(A在B的左侧),且A、B两点经折叠后重合,求A、B两点表示的数是多少?
(2)若点D表示的数为x,则当x为_______时,|x+1|与|x﹣2|的值相等.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在我市美化工程招标时,有甲、乙两个工程队投标.经测算:甲队单独完成这项工程需要60天;若由甲队先做20天,剩下的工程由甲、乙合做24天可完成.
(1)乙队单独完成这项工程需要多少天?
(2)甲队施工一天,需付工程款3.5万元,乙队施工一天需付工程款2万元.若该工程计划在70天内完成,在不超过计划天数的前提下,是由甲队或乙队单独完成该工程省钱?还是由甲乙两队全程合作完成该工程省钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某农产品生产基地收获红薯192吨,准备运给甲、乙两地的承包商进行包销.该基地用大、小两种货车共18辆恰好能一次性运完这批红薯,已知这两种货车的载重量分别为14吨/吨和8吨/辆,运往甲、乙两地的运费如下表:
车型
运费
运往甲地/(元/辆)
运往乙地/(元/辆)
大货车
720
800
小货车
500
650
(1)求这两种货车各用多少辆;
(2)如果安排10辆货车前往甲地,其余货车前往乙地,其中前往甲地的大货车为a辆,总运费为w元,求w关于a的函数关系式;
(2)在(2)的条件下,若甲地的承包商包销的红薯不少于96吨,请你设计出使总运费最低的货车调配方案,并求出最低总运费.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,二次函数y=ax2+bx+2的图象与x轴交于A(﹣3,0),B(1,0)两点,与y轴交于点C.

(1)求这个二次函数的关系解析式;
(2)点P是直线AC上方的抛物线上一动点,是否存在点P,使△ACP的面积最大?若存在,求出点P的坐标;若不存在,说明理由;
(3)在平面直角坐标系中,是否存在点Q,使△BCQ是以BC为腰的等腰直角三角形?若存在,直接写出点Q的坐标;若不存在,说明理由;
(4)点Q是直线AC上方的抛物线上一动点,过点Q作QE垂直于x轴,垂足为E.是否存在点Q,使以点B、Q、E为顶点的三角形与△AOC相似?若存在,直接写出点Q的坐标;若不存在,说明理由;
(5)点M为抛物线上一动点,在x轴上是否存在点Q,使以A、C、M、Q为顶点的四边形是平行四边形?若存在,直接写出点Q的坐标;若不存在,说明理由. -
科目: 来源: 题型:
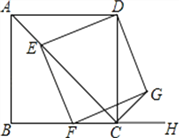
查看答案和解析>>【题目】如图,已知四边形ABCD为正方形,AB=
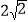 ,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE.交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.
,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE.交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.①求证:矩形DEFG是正方形;
②探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由.
相关试题

