Question

【题目】已知，如图，在Rt△ABC中，∠ACB＝900，AD平分∠CAB交BC于点D，过点C作CE⊥AD，垂足为E，CE的延长线交AB于点F，过点E作EG∥BC交AB于点G， ， ，求：（1）AC的长（2）EG的长．

Answer 1

【答案】（1）4；（2）4

【解析】试题分析：（1）∠CAD是公共角，∠ACB=∠AEC=90°，所以△ACE和△ADC相似，根据相似三角形对应边成比例，列出比例式整理即可得到AC2=AEAD，代入数据计算即可；

（2）根据勾股定理求出BC的长度为8，再根据AD平分∠CAB交BC于点D，CE⊥AD证明△ACE和△AFE全等，根据全等三角形对应边相等，CE=EF，最后根据三角形的中位线平行于第三边并且等于第三边的一半EG=BC．

解：∵CE⊥AD，

∴∠AEC=90°，

∵∠ACB=90°，

∴∠AEC=∠ACB，

又∠CAE=∠CAE，

∴△ACE∽△ADC，

∴AC:AE=AD:AC，

即AC2=AEAD，

∵AEAD=16，

∴AC2=16，

∴AC=4；

(2)在△ABC中,

BC== ，

∵AD平分∠CAB交BC于点D，

∴∠CAE=∠FAE，

∵CE⊥AD，

∴∠AEC=∠AEF=90°，

在△ACE和△AFE中，

，

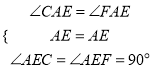∴△ACE≌△AFE(ASA)，

∴CE=EF，

∵EG∥BC，

∴EG=BC=×8=4.