【题目】如图,已知A、B、C是数轴上的三点,点C表示的数是6,点B与点C之间的距离是4,点B与点A的距离是12,点P为数轴上一动点.
(1)数轴上点A表示的数为 .点B表示的数为 ;
(2)数轴上是否存在一点P,使点P到点A、点B的距离和为16,若存在,请求出此时点P所表示的数;若不存在,请说明理由;
(3)点P以每秒1个单位长度的速度从C点向左运动,点Q以每秒2个单位长度从点B出发向左运动,点R从点A以每秒5个单位长度的速度向右运动,它们同时出发,运动的时间为t秒,请求点P与点Q,点R的距离相等时t的值.

参考答案:
【答案】(1)-10;2 (2)存在;﹣12或4 (3)![]() 或4
或4
【解析】
(1)结合数轴可知点A和点B都在点C的左边,且点A小于0,在根据题意列式计算即可得到答案;
(2)因为AB=12,则P不可能在线段AB上,所以分两种情况:
①当点P在BA的延长线上时,②当点P在AB的延长线上时,进行讨论,即可得到答案;
(3)根据题意“t秒P点到点Q,点R的距离相等”,则此时点P、Q、R所表示的数分别是6﹣t,2﹣2t,﹣10+5t,分①6﹣t﹣(2﹣2t)=6﹣t﹣(﹣10+5t),②6﹣t﹣(2﹣2t)=(﹣10+5t)﹣(6﹣t)两种情况,计算即可得到答案.
解:(1)由题意可知点A和点B都在点C的左边,且点A小于0,则由题意可得数轴上点B表示的数为6-4=2,点A表示的数为2-10=﹣10,故答案为:﹣10,2;
(2)∵AB=12,
∴P不可能在线段AB上,
所以分两种情况:
①如图1,当点P在BA的延长线上时,PA+PB=16,

∴PA+PA+AB=16,
2PA=16﹣12=4,
PA=2,
则点P表示的数为﹣12;
②如图2,当点P在AB的延长线上时,同理得PB=2,

则点P表示的数为4;
综上,点P表示的数为﹣12或4;
(3)由题意得:t秒P点到点Q,点R的距离相等,则此时点P、Q、R所表示的数分别是6﹣t,2﹣2t,﹣10+5t,
①6﹣t﹣(2﹣2t)=6﹣t﹣(﹣10+5t),解得t=![]() ;
;
②6﹣t﹣(2﹣2t)=(﹣10+5t)﹣(6﹣t),解得t=4;
答:点P与点Q,点R的距离相等时t的值是![]() 或4秒.
或4秒.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道,有理数包括整数、有限小数和无限循环小数,事实上,所有的有理数都可以化为分数形式(整数可看作分母为1的分数),那么无限循环小数如何表示为分数形式呢?请看以下示例:
例:将
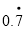 化为分数形式,
化为分数形式,由于
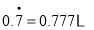 ,设
,设 ,①
,①得
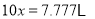 ,②
,②②①得
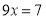 ,解得
,解得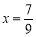 ,于是得
,于是得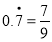 .
.同理可得
 ,
,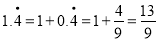 .
.根据以上阅读,回答下列问题:(以下计算结果均用最简分数表示)
(类比应用)
(1)
 ;
;(2)将
 化为分数形式,写出推导过程;
化为分数形式,写出推导过程;(迁移提升)
(3)
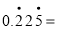 ,
,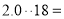 ;(注
;(注 ,
,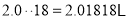 )
)(拓展发现)
(4)若已知
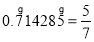 ,则
,则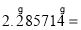 .
. -
科目: 来源: 题型:
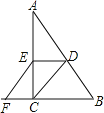
查看答案和解析>>【题目】已知,如图,在Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,F是BC延长线上的一点,且EF∥DC.(1)求证:四边形CDEF是平行四边形;(2)若EF=2cm,求AB的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AD∥BC,AB⊥AC,点E是BC的中点,AE与BD交于点F,且F是AE的中点.
(Ⅰ)求证:四边形AECD是菱形;(Ⅱ)若AC=4,AB=5,求四边形ABCD的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,点O为AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的外角平分线CF于点F,交∠ACB内角平分线CE于E.

(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论;
(3)若AC边上存在点O,使四边形AECF是正方形,猜想△ABC的形状并证明你的结论。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,C是线段AB上一点,M是线段AC的中点,N是线段BC的中点.
(1)如果AB=20 cm,AM=6 cm,求NC的长;
(2)如果MN=6 cm,求AB的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】请仔细阅读下面材料,然后解决问题:
在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”.例如:
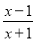 ,
, 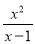 ;当分子的次数小于分母的次数时,我们称之为“真分式”,例如:
;当分子的次数小于分母的次数时,我们称之为“真分式”,例如: 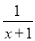 ,
, 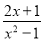 .我们知道,假分数可以化为带分数,例如:
.我们知道,假分数可以化为带分数,例如: 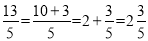 ,类似的,假分式也可以化为“带分式”(整式与真分式和的形式),例如:
,类似的,假分式也可以化为“带分式”(整式与真分式和的形式),例如:  .
.(1)将分式
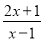 化为带分式;
化为带分式;(2)当x取哪些整数值时,分式
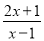 的值也是整数?
的值也是整数?(3)当x的值变化时,分式
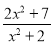 的最大值为 .
的最大值为 .
相关试题

