Question

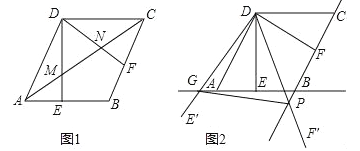
【题目】(2016山东潍坊第24题)如图，在菱形ABCD中，AB=2，∠BAD=60°，过点D作DE⊥AB于点E，DF⊥BC于点F．

（1）如图1，连接AC分别交DE、DF于点M、N，求证：MN=AC；

（2）如图2，将△EDF以点D为旋转中心旋转，其两边DE′、DF′分别与直线AB、BC相交于点G、P，连接GP，当△DGP的面积等于3时，求旋转角的大小并指明旋转方向．

Answer 1

【答案】（1）详见解析；（2）将△EDF以点D为旋转中心，顺时针或逆时针旋转60°时，△DGP的面积等于3．

【解析】

试题分析：（1）连接BD，易证△ABD为等边三角形，由等腰三角形的三线合一得到AE=EB，根据相似三角形的性质解答即可；（2）分∠EDF顺时针旋转和逆时针旋转两种情况，根据旋转变换的性质解答即可．

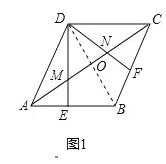
试题解析：（1）证明：如图1，连接BD，交AC于O，

在菱形ABCD中，∠BAD=60°，AD=AB，

∴△ABD为等边三角形，

∵DE⊥AB，

∴AE=EB，

∵AB∥DC，

∴==，

同理， =，

∴MN=AC；

（2）解：∵AB∥DC，∠BAD=60°，

∴∠ADC=120°，又∠ADE=∠CDF=30°，

∴∠EDF=60°，

当∠EDF顺时针旋转时，

由旋转的性质可知，∠EDG=∠FDP，∠GDP=∠EDF=60°，

DE=DF=，∠DEG=∠DFP=90°，

在△DEG和△DFP中，

，

∴△DEG≌△DFP，

∴DG=DP，

∴△DGP为等边三角形，

∴△DGP的面积=DG2=3，

解得，DG=2，

则cos∠EDG==，

∴∠EDG=60°，

∴当顺时针旋转60°时，△DGP的面积等于3，

同理可得，当逆时针旋转60°时，△DGP的面积也等于3，

综上所述，将△EDF以点D为旋转中心，顺时针或逆时针旋转60°时，△DGP的面积等于3．