【题目】如图,四边形ABCD 内接于⊙O,BD是⊙O的直径,过点A作⊙O的切线AE交CD的延长线于点E,DA平分∠BDE.
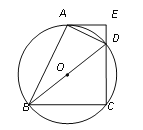
(1)求证:AE⊥CD;
(2)已知AE=4cm,CD=6cm,求⊙O的半径.
参考答案:
【答案】(1)证明见解析;(2)5cm.
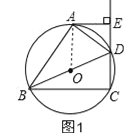
【解析】试题分析:(1)连接OA,因为点A在⊙O上,所以只要证明OA⊥AE即可;由同圆的半径相等得:OA=OD,则∠ODA=∠OAD,根据角平分线可知:∠OAD=∠EDA,所以EC∥OA,由此得OA⊥AE,则AE是⊙O的切线;
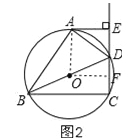
(2)过点O作OF⊥CD,垂足为点F,证明四边形AOFE是矩形,得OF=AE=4cm,由垂径定理得:DF=3,根据勾股定理求半径OD的长.
试题解析:
(1)连结OA,∵OA=OD,
∴∠ODA=∠OAD,
∵DA平分∠BDE,
∴∠ODA=∠EDA,
∴∠OAD=∠EDA,
∴EC∥OA,
∵AE⊥CD,
∴OA⊥AE,
∵点A在⊙O上,
∴AE是⊙O的切线;
(2)过点O作OF⊥CD,垂足为点F,
∵∠OAE=∠AED=∠OFD=90°,
∴四边形AOFE是矩形,
∴OF=AE=4cm,
又∵OF⊥CD,
∴DF=![]() CD=3cm,
CD=3cm,
在Rt△ODF中,OD=![]() =5cm,
=5cm,
即⊙O的半径为5cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2+3x+1﹣m=0有两个不相等的实数根.
(1)求m的取值范围;
(2)若m为负整数,求此时方程的根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一列长a米的队伍以每分钟60米的速度向前行进,队尾一名同学用1分钟从队尾走到队头,为_____米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知am=4,an=16,那么am+n的值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小说《流浪地球》中提到“华北794号地球发动机,全功率运行时能向大地产生1500000000吨的推力”,这里的数据15000000000科学记数法表示为( )
A. 1.5×1012B. 1.5×1011C. 1.5×1010D. 150×108
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次800米的长跑比赛中,甲、乙两人所跑的路程s(米)与各自所用时间t(秒)之间的函数图象分别为线段OA和折线OBCD,则下列说法正确的是( )
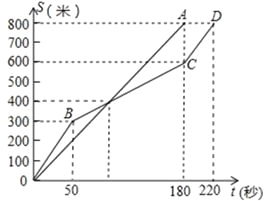
A. 甲的速度随时间的增加而增大
B. 乙的平均速度比甲的平均速度大
C. 在起跑后第180秒时,两人相遇
D. 在起跑后第50秒时,乙在甲的前面
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)先化简,再求值: (a+1)2-(3a2+a)÷a,其中a=-3.
(2)已知x+y=3,xy=-2. 求(x-1)(y-1)的值.
相关试题

