【题目】抛物线![]() 的顶点在直线
的顶点在直线![]() 上,过点F
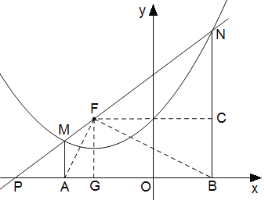
上,过点F![]() 的直线与抛物线交于M、N两点(点M在点N的左边),MA⊥
的直线与抛物线交于M、N两点(点M在点N的左边),MA⊥![]() 轴于点A,NB⊥
轴于点A,NB⊥![]() 轴于点B.
轴于点B.

(1)先通过配方求抛物线的顶点坐标(坐标可用含![]() 的代数式表示),再求
的代数式表示),再求![]() 的值;
的值;
(2)设点N的横坐标为![]() ,试用含
,试用含![]() 的代数式表示点N的纵坐标,并说明NF=NB;
的代数式表示点N的纵坐标,并说明NF=NB;
(3)若射线NM交![]() 轴于点P,且PA×PB=
轴于点P,且PA×PB=![]() ,求点M的坐标.
,求点M的坐标.
参考答案:
【答案】(1)顶点坐标为(-2 , ![]() ),
),![]() =2;(2)N(a,
=2;(2)N(a,![]() );(3)M(-3 ,
);(3)M(-3 ,![]() ).
).
【解析】
试题分析:(1)利用配方法将二次函数整理成顶点式即可,再利用点在直线上的性质得出答案即可;
(2)首先利用点N在抛物线上,得出N点坐标,再利用勾股定理得出NF2=NC2+FC2,进而得出NF2=NB2,即可得出答案;
(3)求点M的坐标,需要先求出直线PF的解析式.首先由(2)的思路得出MF=MA,然后连接AF、FB,通过证明△PFA∽△PBF,利用相关的比例线段将PAPB的值转化为PF的值,进而求出点F的坐标和直线PF的解析式,即可得解.
试题解析:(1)![]()
∴顶点坐标为(-2 , ![]() )
)
∵顶点在直线![]() 上,
上,
∴-2+3=![]() ,
,
得![]() =2
=2
(2)∵点N在抛物线上,
∴点N的纵坐标为![]()
即点N(a,![]() )
)
过点F作FC⊥NB于点C,
在Rt△FCN中,FC=![]() +2,NC=NB-CB=
+2,NC=NB-CB=![]() ,
,![]()
∴![]()
而![]() =
=![]() =
=![]()
∴![]() =
=![]() ,NF=NB
,NF=NB
(3)连结AF、BF
由NF=NB,得∠NFB=∠NBF,
由(2)的结论知,MF=MA,∴∠MAF=∠MFA,
∵MA⊥x轴,NB⊥x轴,∴MA∥NB,∴∠AMF+∠BNF=180°
∵△MAF和△NFB的内角总和为360°,
∴2∠MAF+2span>∠NBF=180°,∠MAF+∠NBF=90°
∵∠MAB+∠NBA=180°,
∴∠FBA+∠FAB=90°
又∵∠FAB+∠MAF=90°
∴∠FBA=∠MAF=∠MFA
又∵∠FPA=∠BPF,
∴△PFA∽△PBF,
∴![]()
过点F作FG⊥![]() 轴于点G,在Rt△PFG中,PG=
轴于点G,在Rt△PFG中,PG=![]() =
=![]() ,
,
∴PO=PG+GO=![]() ,
,
∴P(-![]() , 0)
, 0)
设直线PF:y=kx+b把点F(-2 , 2)、点P(-![]() , 0)代入y=kx+b
, 0)代入y=kx+b
解得![]() =
=![]() ,
,![]() =
=![]() ,
,
∴直线PF:![]()
解方程![]() ,得
,得![]() =-3或
=-3或![]() =2(不合题意,舍去)
=2(不合题意,舍去)
当![]() =-3时,
=-3时,![]() =
=![]() ,
,
∴M(-3 ,![]() )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线AB交⊙O于C、D两点,CE是⊙O的直径,CF平分∠ACE交⊙O于点F,连接EF,过点F作FG∥ED交AB于点G.
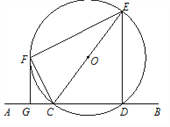
(1)求证:直线FG是⊙O的切线;
(2)若FG=4,⊙O的半径为5,求四边形FGDE的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,∠AOB是平角,∠AOC=30°,∠BOD=60°,OM,ON分别是∠AOC,∠BOD的平分线,∠MON等于________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)将下列各数填在相应的集合里.
﹣(﹣2.5),(﹣1)2,﹣|﹣2|,﹣22,0,
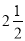 ,﹣1.5;
,﹣1.5;正数集合{ …}
分数集合{ …}
(2)把表示上面各数的点画在数轴上,再按从小到大的顺序,用“<“号把这些数连接起来.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列诗句表述的是随机事件的是( )
A.离离原上草,一岁一枯荣B.危楼高百尺,手可摘星辰
C.会当凌绝顶,一览众山小D.东边日出西边雨,道是无晴却有晴
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正六边形的边长为10,那么它的外接圆的半径为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
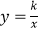 的图象经过点(2,3),下列说法正确的是( )
的图象经过点(2,3),下列说法正确的是( )
A.y随x的增大而增大
B.函数的图象只在第一象限
C.当x<0时,必有y<0
D.点(﹣2,﹣3)不在此函数图象上
相关试题

