【题目】如图,直线AB与CD相交于点O,∠BOE=∠DOF=90°.
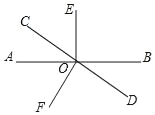
(1)写出图中与∠COE互补的所有的角(不用说明理由).
(2)问:∠COE与∠AOF相等吗?请说明理由;
(3)如果∠AOC=![]() ∠EOF,求∠AOC的度数.
∠EOF,求∠AOC的度数.
参考答案:
【答案】(1) ∠DOE,∠BOF;(2) 相等;(3) ∠AOC=30°.
【解析】试题分析:
(1)由题意易得∠COE+∠DOE=180°,由∠BOE=∠DOF=90°可得∠DOE=∠BOF,从而可得∠COE的补角是∠DOE和∠BOF;
(2)由∠BOE=∠DOF=90°易得∠AOE=∠COF=90°,从而可得∠COE=∠AOF;
(3)设∠AOC=x,则可得∠EOF=5x,结合∠COE=∠AOF可得∠COE=2x,由∠AOC+∠COE=∠AOE=90°列出关于x的方程,解方程求得x的值即可.
试题解析;
(1)∵直线AB与CD相交于点O,
∴∠COE+∠DOE=180°,即∠DOE是∠COE的补角,
∵∠BOE=∠DOF=90°,
∴∠BOE+∠BOD=∠DOF+∠BOD,
即:∠DOE=∠BOF,
∴与∠COE互补的角有:∠DOE,∠BOF;
(2)∠COE与∠AOF相等,
理由:∵直线AB、CD相交于点O,
∴∠AOE+∠BOE=180°,∠COF+∠DOF=180°,
又∵∠BOE=∠DOF=90°,
∴∠AOE=∠COF=90°,
∴∠AOE﹣∠AOC=∠COF﹣∠AOC,
∴∠COE=∠AOF;
(3)设∠AOC=x,则∠EOF=5x,
∴∠COE+∠AOF=∠EOF-∠AOC=5x-x=4x,
∵∠COE=∠AOF,
∴∠COE=∠AOF=2x,
∵∠AOE=90°,
∴x+2x=90°,
∴x=30°,
∴∠AOC=30°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为鼓励大学生创业,政府制定了小型企业的优惠政策,许多小型企业应运而生.某市统计了该市2015年1﹣5月新注册小型企业的数量,并将结果绘制成如图两种不完整的统计图:

(1)某市2015年1﹣5月份新注册小型企业一共 家,请将折线统计图补充完整.
(2)该市2015年3月新注册小型企业中,只有2家是养殖企业,现从3月新注册的小型企业中随机抽取2家企业了解其经营情况.请以列表或画树状图的方法求出所抽取的2家企业恰好都是养殖企业的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=5,AC=9,S△ABC=
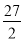 ,动点P从A点出发,沿射线AB方向以每秒5个单位的速度运动,动点Q从C点出发,以相同的速度在线段AC上由C向A运动,当Q点运动到A点时,P、Q两点同时停止运动,以PQ为边作正方形PQEF(P、Q、E、F按逆时针排序),以CQ为边在AC上方作正方形QCGH.
,动点P从A点出发,沿射线AB方向以每秒5个单位的速度运动,动点Q从C点出发,以相同的速度在线段AC上由C向A运动,当Q点运动到A点时,P、Q两点同时停止运动,以PQ为边作正方形PQEF(P、Q、E、F按逆时针排序),以CQ为边在AC上方作正方形QCGH.
(1)求tanA的值;
(2)设点P运动时间为t,正方形PQEF的面积为S,请探究S是否存在最小值?若存在,求出这个最小值,若不存在,请说明理由;
(3)当t为何值时,正方形PQEF的某个顶点(Q点除外)落在正方形QCGH的边上,请直接写出t的值.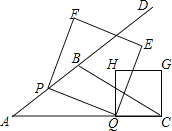
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个两位数,个位数字是x,十位数字是y,将个位和十位数字对调后,所得到新的两位数,与原两位数相加的和是110,可以列方程为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果关于x的不等式组
 的解集为x<﹣2,且使关于x的分式方程
的解集为x<﹣2,且使关于x的分式方程  +
+  =2的解为非负数的所有整数a的个数为( )
=2的解为非负数的所有整数a的个数为( )
A.7个
B.6个
C.5个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】综合题。
(1)解分式方程:
(2)已知 ,求分式
,求分式  的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】单项式-4ab2的系数是( ).
A.4
B.-4
C.3
D.2
相关试题

