【题目】已知:![]() ,OB,OM,ON是
,OB,OM,ON是![]() 内的射线.
内的射线.
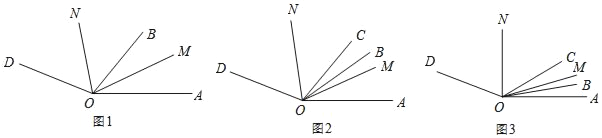
![]() 如图1,若OM平分
如图1,若OM平分![]() ,ON平分
,ON平分![]() 当射线OB绕点O在
当射线OB绕点O在![]() 内旋转时,
内旋转时,![]() ______度
______度![]()
![]() 也是
也是![]() 内的射线,如图2,若
内的射线,如图2,若![]() ,OM平分
,OM平分![]() ,ON平分
,ON平分![]() ,当
,当![]() 绕点O在
绕点O在![]() 内旋转时,求
内旋转时,求![]() 的大小.
的大小.
![]() 在
在![]() 的条件下,若
的条件下,若![]() ,当
,当![]() 在
在![]() 绕O点以每秒
绕O点以每秒![]() 的速度逆时针旋转t秒,如图3,若
的速度逆时针旋转t秒,如图3,若![]() :
:![]() :3,求t的值.
:3,求t的值.

参考答案:
【答案】(1) 80;(2) 70°;(3)t为21秒.
【解析】
(1)因为∠AOD=160°,OB、OC、OM、ON是∠AOD内的射线.若OM平分∠AOB,ON平分∠BOD,则![]() 然后根据关系转化求出角的度数;
然后根据关系转化求出角的度数;
(2)利用各角的关系求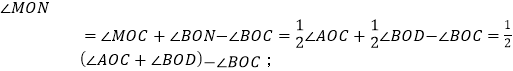
(3)由题意得![]()
由此列出方程求解即可.
解:(1)∵OM平分∠AOB,ON平分∠BOD,
∴![]()
∴∠MON=∠BOM+∠BON
![]()
![]()
=80°,
故答案为:80;
(2)∵OM平分∠AOC,ON平分∠BOD,
∴![]()
即∠MON=∠MOC+∠BON﹣∠BOC
![]()
![]()
![]()
![]()
![]()
=70°;
![]()
又∵∠AOM:∠DON=2:3,
∴3(30°+2t)=2(150°﹣2t),
得t=21.
答:t为21秒.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,点O是等边△ABC内的任一点,连接OA,OB,OC.
(1)如图1,已知∠AOB=150°,∠BOC=120°,将△BOC绕点C按顺时针方向旋转60°得△ADC.
①∠DAO的度数是多少?
②用等式表示线段OA,OB,OC之间的数量关系,并证明;
(2)设∠AOB=α,∠BOC=β.
①当α,β满足什么关系时,OA+OB+OC有最小值?请在图2中画出符合条件的图形,并说明理由;
②若等边△ABC的边长为1,直接写出OA+OB+OC的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,定义点P(x,y)的变换点为P′(x+y,x﹣y).
(1)如图1,如果⊙O的半径为2 ,
,
①请你判断M(2,0),N(﹣2,﹣1)两个点的变换点与⊙O的位置关系;
②若点P在直线y=x+2上,点P的变换点P′在⊙O的内,求点P横坐标的取值范围.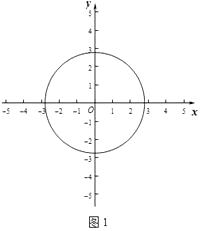
(2)如图2,如果⊙O的半径为1,且P的变换点P′在直线y=﹣2x+6上,求点P与⊙O上任意一点距离的最小值.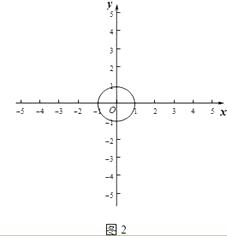
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列关系式不正确的是( )

A.abc<0
B.a+b+c<0
C.2a﹣b>0
D.4a﹣b+c<0 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知数轴上点A表示的数为6,B是数轴上一点,且AB=10,动点P从点A出发,以每秒6个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒,
(1)写出数轴上点B所表示的数 ;
(2)点P所表示的数 ;(用含t的代数式表示);
(3)M是AP的中点,N为PB的中点,点P在运动的过程中,线段MN的长度是否发生变化?若变化,说明理由;若不变,请你画出图形,并求出线段MN的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,点D在边BC所在的直线上,过点D作DF∥AC交直线AB于点F,DE∥AB交直线AC于点E.
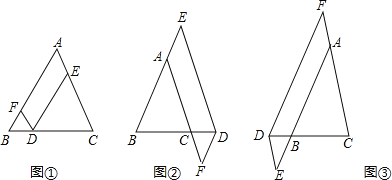
(1)当点D在边BC上时,如图①,求证:DE+DF=AC.
(2)当点D在边BC的延长线上时,如图②;当点D在边BC的反向延长线上时,如图③,请分别写出图②、图③中DE,DF,AC之间的数量关系,不需要证明.
(3)若AC=6,DE=4,则DF= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】近两年,国际市场黄金价格涨幅较大,中国交通银行推出“沃德金”的理财产品,即以黄金为投资产品,投资者从黄金价格的上涨中赚取利润.上周五黄金的收盘价为
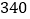 元/克,下表是本周星期一至星期五黄金价格的变化情况.(注:星期一至星期五开市,星期六、星期日休市)
元/克,下表是本周星期一至星期五黄金价格的变化情况.(注:星期一至星期五开市,星期六、星期日休市)星期
一
二
三
四
五
收盘价的变化(与前一天收盘价比较)
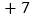

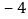
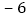
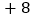
问
 本周星期三黄金的收盘价是多少?
本周星期三黄金的收盘价是多少? 本周黄金收盘时的最高价、最低价分别是多少?
本周黄金收盘时的最高价、最低价分别是多少? 上周,小王以周五的收盘价
上周,小王以周五的收盘价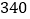 元/克买入黄金
元/克买入黄金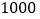 克,已知买入与卖出时均需支付成交金额的千分之五的交易费,卖出黄金时需支付成交金额的千分之三的印花税.本周,小王以周五的收盘价全部卖出黄金
克,已知买入与卖出时均需支付成交金额的千分之五的交易费,卖出黄金时需支付成交金额的千分之三的印花税.本周,小王以周五的收盘价全部卖出黄金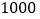 克,他的收益情况如何?
克,他的收益情况如何?
相关试题

