【题目】如图，⊙O与Rt△ABC的斜边AB相切于点D，与直角边AC相交于E、F两点，连结DE，已知∠B=30°，⊙O的半径为12，弧DE的长度为4π．

（1）求证：DE∥BC；

（2）若AF=CE，求线段BC的长度．

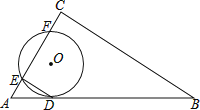
【答案】（1）证明见解析；（2）60.

【解析】（1）证明：如图，连接OE、OD．

∵弧DE的长度为4π，⊙O的半径r＝12，

∴，

∴n＝60，即∠EOD＝60°．

∵OE＝OD，∴∠EDO＝60°，∵AB与⊙O相切于点D，

∴∠ADO＝90°，∴∠ADE＝30°，

∵∠B＝30°，∴∠ADE＝∠B，∴DE∥BC．

（2）如图，作OG⊥AC于G，连接FO，

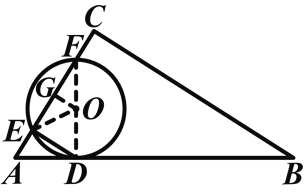
∴EG＝FG．

∵DE∥BC，∠C＝90°，∴∠FED＝90°，∴FD是⊙O的直径，

∴，∵∠A＝60°，ED＝12，∠AED＝90°，

∴， ，

∵∠FDA＝90°，∴，

∴，∵AF＝CE，∴，

∴，∴．

关闭