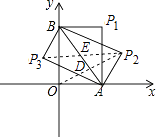
【题目】如图,在平面直角坐标系中,A、B两点分别在x轴、y轴上,OA=3,OB=4,连接AB.点P在平面内,若以点P、A、B为顶点的三角形与△AOB全等(点P与点O不重合),则点P的坐标为 . 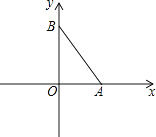
参考答案:
【答案】(3,4)或( ![]() ,
, ![]() )或(﹣
)或(﹣ ![]() ,
, ![]() )
)
【解析】解:如图所示:
①∵OA=3,OB=4,
∴P1(3,4);
②连结OP2 ,
设AB的解析式为y=kx+b,则![]() ,
,
解得 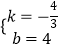 .
.
故AB的解析式为y=﹣ ![]() x+4,
x+4,
则OP2的解析式为y= ![]() x,
x,
联立方程组得 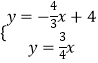 ,
,
解得 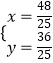 ,
,
则P2( ![]() ,
, ![]() );
);
③连结P2P3 ,
∵(3+0)÷2=1.5,
(0+4)÷2=2,
∴E(1.5,2),
∵1.5×2﹣ ![]() =﹣
=﹣ ![]() ,
,
2×2﹣ ![]() =
= ![]() ,
,
∴P3(﹣ ![]() ,
, ![]() ).
).
故点P的坐标为(3,4)或( ![]() ,
, ![]() )或(﹣
)或(﹣ ![]() ,
, ![]() ).
).
故答案为:(3,4)或( ![]() ,
, ![]() )或(﹣
)或(﹣ ![]() ,
, ![]() ).
).
本题考查了全等三角形的性质及坐标与图形的性质,做这种题要求对全等三角形的判定方法熟练掌握.由条件可知AB为两三角形的公共边,且△AOB为直角三角形,当△AOB和△APB全等时,则可知△APB为直角三角形,再分三种情况进行讨论,可得出P点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=6,EF=2,则BC长为( )

A.8
B.10
C.12
D.14 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE、BE分别交于点G、H,∠CBE=∠BAD.有下列结论:①FD=FE;②AH=2CD;③BCAD=
 AE2;④S△ABC=4S△ADF . 其中正确的有( )
AE2;④S△ABC=4S△ADF . 其中正确的有( )
A.1个
B.2 个
C.3 个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD边长为3,连接AC,AE平分∠CAD,交BC的延长线于点E,FA⊥AE,交CB延长线于点F,则EF的长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:4sin60°+|3﹣
 |﹣(
|﹣(  )﹣1+(π﹣2016)0 .
)﹣1+(π﹣2016)0 . -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形).
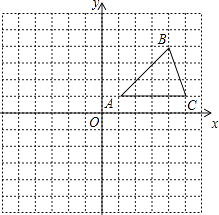
(1)将△ABC沿x轴方向向左平移6个单位,画出平移后得到的△A1B1C1;
(2)将△ABC绕着点A顺时针旋转90°,画出旋转后得到的△AB2C2 , 并直接写出点B2、C2的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了促进学生多样化发展,某校组织开展了社团活动,分别设置了体育类、艺术类、文学类及其它类社团(要求人人参与社团,每人只能选择一项).为了解学生喜爱哪种社团活动,学校做了一次抽样调查.根据收集到的数据,绘制成如下两幅不完整的统计图,请根据图中提供的信息,完成下列问题:

(1)此次共调查了多少人?
(2)求文学社团在扇形统计图中所占圆心角的度数;
(3)请将条形统计图补充完整;
(4)若该校有1500名学生,请估计喜欢体育类社团的学生有多少人?
相关试题

