【题目】把下列各式分解因式:
(1)(b﹣a)2+a(a﹣b)+b(b﹣a);
(2)(x2+4)2﹣16x2.
参考答案:
【答案】(1)2(b﹣a)2;(2)(x+2)2(x﹣2)2
【解析】分析:(1)把括号内的式子化为b-a的形式,再提公因式;(2)先平方差公式,再用完全平方公式分解因式.
详解:(1)(b﹣a)2+a(a﹣b)+b(b﹣a)
=(b﹣a)2﹣a(b﹣a)+b(b﹣a)
=(b﹣a)(b﹣a﹣a+b)
=(b﹣a)(2b﹣2a)
=2(b﹣a)2;
(2)(x2+4)2﹣16x2,
=(x2+4+4x)(x2+4﹣4x)
=(x+2)2(x﹣2)2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读:如图1,点P(x,y)在平面直角坐标中,过点P作PA⊥x轴,垂足为A,将点P绕垂足A顺时针旋转角α(0°<α<90°)得到对应点P′,我们称点P到点P′的运动为倾斜α运动.例如:点P(0,2)倾斜30°运动后的对应点为P′(1,
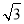 ).
).图形E在平面直角坐标系中,图形E上的所有点都作倾斜α运动后得到图形E′,这样的运动称为图形E的倾斜α运动.
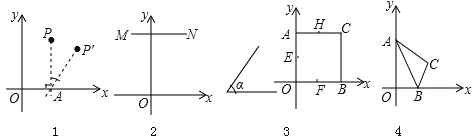
理解
(1)点Q(1,2)倾斜60°运动后的对应点Q′的坐标为 ;
(2)如图2,平行于x轴的线段MN倾斜α运动后得到对应线段M′N′,M′N′与MN平行且相等吗?说明理由.
应用:(1)如图3,正方形AOBC倾斜α运动后,其各边中点E,F,G,H的对应点E′,F′,G′,H′构成的四边形是什么特殊四边形: ;
(2)如图4,已知点A(0,4),B(2,0),C(3,2),将△ABC倾斜α运动后能不能得到Rt△A′B′C′,且∠A′C′B′为直角,其中点A′,B′,C′为点A,B,C的对应点.请求出cosα的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】遵义市某学校7位学生的中考体育测试成绩(满分40分)依次为37,40,39,37,40,38,40.则这组数据的众数与中位数分别是( )
A. 40,37B. 40,39C. 39,40D. 40,38
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,真命题是( )
A.对角线相等的四边形是菱形B.有一组邻边相等的平行四边形是菱形
C.四条边相等的四边形是矩形D.对角线互相垂直的平行四边形是矩形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,△ABC中,AH⊥BC于H,E,D,F分别是AB,BC,AC的中点,则四边形EDHF是( )
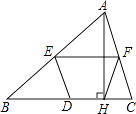
A.一般梯形
B.等腰梯形
C.直角梯形
D.直角等腰梯形 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,梯形OABC中,O为直角坐标系的原点,A、B、C的坐标分别为(14,0)、(14,3)、(4,3).点P、Q同时从原点出发,分别作匀速运动,其中点P沿OA向终点A运动,速度为每秒1个单位;点Q沿OC、CB向终点B运动,当这两点中有一点到达自己的终点时,另一点也停止运动.设P从出发起运动了t秒.
(1)如果点Q的速度为每秒2个单位,①试分别写出这时点Q在OC上或在CB上时的坐标(用含t的代数式表示,不要求写出t的取值范围);
②求t为何值时,PQ∥OC?
(2)如果点P与点Q所经过的路程之和恰好为梯形OABC的周长的一半,①试用含t的代数式表示这时点Q所经过的路程和它的速度;
②试问:这时直线PQ是否可能同时把梯形OABC的面积也分成相等的两部分?如有可能,求出相应的t的值和P、Q的坐标;如不可能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD,直线EF与AB,CD分别交于点 M,N,过点N的直线GH 与AB交于点P,则下列结论中一定正确的个数是( )
①∠EMB=∠MND;②∠BMN=∠MNC;③∠CNH=∠BPG;④∠DNG=∠AME.
A.1个
B.2个
C.3个
D.4个
相关试题

