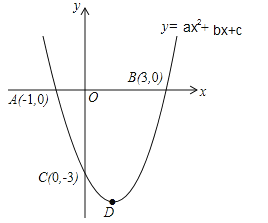
【题目】如图,抛物线![]() 的图象与x轴交于A(﹣1.0),B(3,0)两点,与y轴交于点C(0,﹣3),顶点为D.
的图象与x轴交于A(﹣1.0),B(3,0)两点,与y轴交于点C(0,﹣3),顶点为D.
(1)求此抛物线的解析式.
(2)求此抛物线顶点D的坐标和对称轴.
(3)探究对称轴上是否存在一点P,使得以点P、D、A为顶点的三角形是等腰三角形?若存在,请求出所有符合条件的P点的坐标,若不存在,请说明理由.
参考答案:
【答案】(1)![]() ;(2)D的坐标是(1,﹣4),对称轴是直线x=1;(3)P(1,
;(2)D的坐标是(1,﹣4),对称轴是直线x=1;(3)P(1, ![]() )或(1,
)或(1, ![]() )或(1,
)或(1, ![]() )或(1,4).
)或(1,4).
【解析】试题分析:(1)根据抛物线![]() 的图象与x轴交于A(﹣1.0),B(3,0)两点,与y轴交于点C(0,﹣3),可以求得抛物线的解析式;
的图象与x轴交于A(﹣1.0),B(3,0)两点,与y轴交于点C(0,﹣3),可以求得抛物线的解析式;
(2)根据(1)中的解析式化为顶点式,即可得到此抛物线顶点D的坐标和对称轴;
(3)首先写出存在,然后运用分类讨论的数学思想分别求出各种情况下点P的坐标即可.
试题解析:(1)∵抛物线![]() 的图象与x轴交于A(﹣1.0),B(3,0)两点,与y轴交于点C(0,﹣3),∴
的图象与x轴交于A(﹣1.0),B(3,0)两点,与y轴交于点C(0,﹣3),∴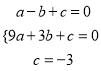 ,解得:
,解得: 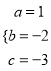 ,即此抛物线的解析式是
,即此抛物线的解析式是![]() ;
;
(2)∵![]() =
=![]() ,∴此抛物线顶点D的坐标是(1,﹣4),对称轴是直线x=1;
,∴此抛物线顶点D的坐标是(1,﹣4),对称轴是直线x=1;
(3)存在一点P,使得以点P、D、A为顶点的三角形是等腰三角形,设点P的坐标为(1,y),分三种情况讨论:
①当PA=PD时![]() =
=![]() ,解得,y=
,解得,y=![]() ,即点P的坐标为(1,
,即点P的坐标为(1, ![]() );
);
②当DA=DP时, ![]() =
=![]() ,解得,y=
,解得,y=![]() ,即点P的坐标为(1,
,即点P的坐标为(1, ![]() )或(1,
)或(1, ![]() );
);
③当AD=AP时, ![]() =
=![]() ,解得,y=±4,即点P的坐标是(1,4)或(1,﹣4),当点P为(1,﹣4)时与点D重合,故不符合题意.
,解得,y=±4,即点P的坐标是(1,4)或(1,﹣4),当点P为(1,﹣4)时与点D重合,故不符合题意.
由上可得,以点P、D、A为顶点的三角形是等腰三角形时,点P的坐标为(1, ![]() )或(1,
)或(1, ![]() )或(1,
)或(1, ![]() )或(1,4).
)或(1,4).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某天股票A开盘价为36元,上午10时跌1.5元,中午2时跌0.5元,下午收盘时又涨了0.3元,该股票今天的收盘价是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】李老师的存储卡中有5500元,取出1800元,又存入1500元,又取出2200元,这时存储卡中还有______元钱.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种微生物半径约为0.00000637米,该数字用科学记数法可表示为( )
A. 0.637×10﹣5 B. 6.37×10﹣6 C. 63.7×10﹣7 D. 6.37×10﹣7
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个口袋中装有大小完全一样的红、黄、绿三种颜色的玻璃球108个,小明通过多次摸球试验后,发现摸到红球的频率为25%,摸到黄球的频率为45%,摸到绿球的频率为30%,则可估计口袋中有红球____个,有黄球_____个,有绿球_____个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(6分)某商场统计了今年1~5月A,B两种品牌冰箱的销售情况,并将获得的数据绘制成折线统计图.
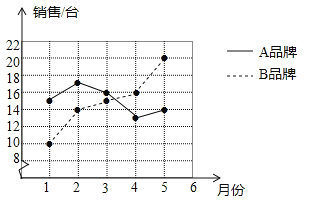
(1)分别求该商场这段时间内A,B两种品牌冰箱月销售量的中位数和方差;
(2)根据计算结果,比较该商场1~5月这两种品牌冰箱月销售量的稳定性.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个物体的质量为1.0549kg,则用四舍五入法将1.0549精确到0.01的近似值为( )
A. 1 B. 1.1 C. 1.05 D. 1.055
相关试题

