【题目】如图,PQ∥MN,A、B分别为直线MN、PQ上两点,且∠BAN=45°,若射线AM绕点A顺时针旋转至AN后立即回转,射线BQ绕点B逆时针旋转至BP后立即回转,两射线分别绕点A、点B不停地旋转,若射线AM转动的速度是a°/秒,射线BQ转动的速度是b°/秒,且a、b满足|a﹣5|+(b﹣1)2=0.(友情提醒:钟表指针走动的方向为顺时针方向)
(1)a= ,b= ;
(2)若射线AM、射线BQ同时旋转,问至少旋转多少秒时,射线AM、射线BQ互相垂直.
(3)若射线AM绕点A顺时针先转动18秒,射线BQ才开始绕点B逆时针旋转,在射线BQ到达BA之前,问射线AM再转动多少秒时,射线AM、射线BQ互相平行?

参考答案:
【答案】(1)a=5,b=1;(2)t=15(s);(3)15,22.5.
【解析】
(1)依据|a﹣5|+(b﹣1)2=0,即可得到a,b的值;
(2)依据∠ABO+∠BAO=90°,∠ABQ+∠BAM=180°,即可得到射线AM、射线BQ第一次互相垂直的时间;
(3)分两种情况讨论,依据∠ABQ'=∠BAM“时,BQ'∥AM“,列出方程即可得到射线AM、射线BQ互相平行时的时间.
解:(1)|a﹣5|+(b﹣1)2=0,
∴a﹣5=0,b﹣1=0,
∴a=5,b=1,
故答案为:5,1;
(2)设至少旋转t秒时,射线AM、射线BQ互相垂直.
如图,设旋转后的射线AM、射线BQ交于点O,则BO⊥AO,
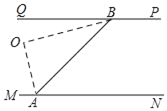
∴∠ABO+∠BAO=90°,
∵PQ∥MN,
∴∠ABQ+∠BAM=180°,
∴∠OBQ+∠OAM=90°,
又∵∠OBQ=t°,∠OAM=5t°,
∴t°+5t°=90°,
∴t=15(s);
(3)设射线AM再转动t秒时,射线AM、射线BQ互相平行.
如图,射线AM绕点A顺时针先转动18秒后,AM转动至AM'的位置,∠MAM'=18×5=90°,
分两种情况:
①当9<t<18时,∠QBQ'=t°,∠M'AM“=5t°,
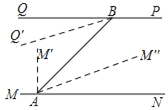
∵∠BAN=45°=∠ABQ,
∴∠ABQ'=45°﹣t°,∠BAM“=5t﹣45°,
当∠ABQ'=∠BAM“时,BQ'∥AM“,
此时,45°﹣t°=5t﹣45°,
解得t=15;
②当18<t<27时,∠QBQ'=t°,∠NAM“=5t°﹣90°,
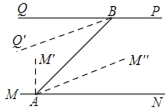
∵∠BAN=45°=∠ABQ,
∴∠ABQ'=45°﹣t°,∠BAM“=45°﹣(5t°﹣90°)=135°﹣5t°,
当∠ABQ'=∠BAM“时,BQ'∥AM“,
此时,45°﹣t°=135°﹣5t,
解得t=22.5;
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校“阳光足球俱乐部”计划购进一批甲、乙两种型号的足球,乙型足球每个进价比甲型足球每个进价多10元,若购进甲型足球3个和乙型足球5个,共需要资金370元.
(1)求甲、乙两种型号的足球进价各是多少元?
(2)该商店计划购进这两种型号的足球共50个,而可用于购买这两种型号的足球资金不少于2250元,但又不超过2270元.该商店有几种进货方案?
(3)已知商店出售一个甲种足球可获利6元,出售一个乙种足球可获利10元,试问在(2)的条件下,商店采用哪种方案可获利最多?
-
科目: 来源: 题型:
查看答案和解析>>【题目】矩形ABCD中,E、F分别是AD、BC的中点,CE、AF分别交BD于G、H两点.
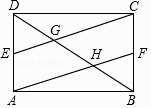
求证:
(1)四边形AFCE是平行四边形;
(2)证明:EG=FH. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校决定组织学生开展校外拓展活动,若每位老师带17个学生,还剩12个学生没人带;若每位老师带18个学生,就有一位老师少带4个学生.现有甲乙两种大客车,它们的载客量和租金如下表所示.学校计划此次拓展活动的租车总费用不超过3100元,为了安全,每辆客车上至少要有2名老师.
客车
甲种
乙种
载客量/(人/辆)
30
42
租 金/(元/辆)
300
400
(1)参加此次拓展活动的老师有 人,参加此次拓展活动的学生有 人;
(2)既要保证所有师生都有车坐,又要保证每辆客车上至少要有2名老师,可知租用客车总数为 辆.
(3)你能得出哪几种不同的租车方案?其中哪种租车方案最省钱?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一张三角形纸片ABC(如图甲),其中AB=AC.将纸片沿过点B的直线折叠,使点C落到AB边上的E点处,折痕为BD(如图乙).再将纸片沿过点E的直线折叠,点A恰好与点D重合,折痕为EF(如图丙).原三角形纸片ABC中,∠ABC的大小为______°.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,E为AB边上一点,EC平分∠DEB,F为CE的中点,连接AF,BF,过点E作EH∥BC分别交AF,CD于G,H两点.

(1)求证:DE=DC;
(2)求证:AF⊥BF;
(3)当AFGF=28时,请直接写出CE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】校学生会对七年级部分学生的课外阅读量进行了随机调查,整理调查结果,并根据调查结果绘制了不完整的图表,如图所示:
本数(本)
频数(人数)
频率
5
a
0.3
6
10
0.2
7
20
b
8
5
0.1
合计
c
1
(1)统计表中的b= ,c= ;请将频数分布直方图补充完整.
(2)所有被调查学生课外阅读的平均本数为 本,课外阅读书本数的中位数为 本.
(3)若该校七年级共有1200名学生,估计该校七年级学生课外阅读6本及以下的人数为 人.

相关试题

