【题目】如图,在平面直角坐标系中,点A,B的坐标分别为(﹣3,0),(0,6).动点P从点O出发,沿x轴正方向以每秒1个单位的速度运动,同时动点C从点B出发,沿射线BO方向以每秒2个单位的速度运动,以CP,CO为邻边构造PCOD,在线段OP延长线上取点E,使PE=AO,设点P运动的时间为t秒.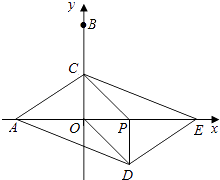
(1)当点C运动到线段OB的中点时,求t的值及点E的坐标;
(2)当点C在线段OB上时,求证:四边形ADEC为平行四边形;
(3)在线段PE上取点F,使PF=1,过点F作MN⊥PE,截取FM=2,FN=1,且点M,N分别在一,四象限,在运动过程中,设PCOD的面积为S.
①当点M,N中有一点落在四边形ADEC的边上时,求出所有满足条件的t的值;
②若点M,N中恰好只有一个点落在四边形ADEC的内部(不包括边界)时,直接写出S的取值范围.
参考答案:
【答案】
(1)
解:∵OB=6,C是OB的中点,
∴BC= ![]() OB=3,
OB=3,
∴2t=3即t= ![]() ,
,
∴OE= ![]() +3=
+3= ![]() ,E(
,E( ![]() ,0)
,0)
(2)
解:如图,连接CD交OP于点G,
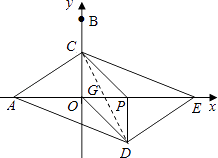
在PCOD中,CG=DG,OG=PG,
∵AO=PE,
∴AG=EG,
∴四边形ADEC是平行四边形.
(3)
解:①(Ⅰ)当点C在BO上时,
第一种情况:如图,当点M在CE边上时,
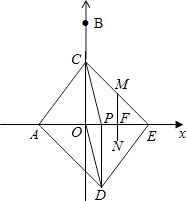
∵MF∥OC,
∴△EMF∽△ECO,
∴ ![]() ,即
,即 ![]() =
= ![]() ,
,
∴t=1,
第二种情况:当点N在DE边时,
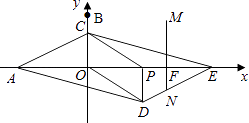
∵NF∥PD,
∴△EFN∽△EPD,
∴ ![]() ,即
,即 ![]() =
= ![]() ,
,
∴t= ![]() ,
,
(Ⅱ)当点C在BO的延长线上时,
第一种情况:当点M在DE边上时,
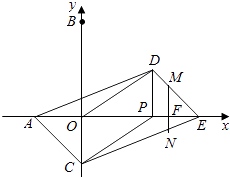
∵MF∥PD,
∴△EMF∽△EDP,
∴ ![]() 即
即 ![]() =
= ![]() ,
,
∴t= ![]() ,
,
第二种情况:当点N在CE边上时,
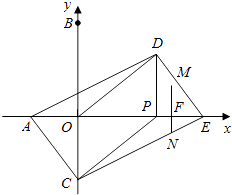
∵NF∥OC,
∴△EFN∽△EOC,
∴ ![]() 即
即 ![]() =
= ![]() ,
,
∴t=5.
② ![]() <S≤
<S≤ ![]() 或
或 ![]() <S≤20.
<S≤20.
当1≤t< ![]() 时,
时,
S=t(6﹣2t)=﹣2(t﹣ ![]() )2+
)2+ ![]() ,
,
∵t= ![]() 在1≤t<
在1≤t< ![]() 范围内,
范围内,
∴ ![]() <S≤
<S≤ ![]() ,
,
当 ![]() <t≤5时,S=t(2t﹣6)=2(t﹣
<t≤5时,S=t(2t﹣6)=2(t﹣ ![]() )2﹣
)2﹣ ![]() ,
,
∴ ![]() <S≤20.
<S≤20.
【解析】(1)由C是OB的中点求出时间,再求出点E的坐标,(2)连接CD交OP于点G,由PCOD的对角线相等,求四边形ADEC是平行四边形.(3)当点C在BO上时,第一种情况,当点M在CE边上时,由△EMF∽△ECO求解,第二种情况,当点N在DE边上时,由△EFN∽△EPD求解;当点C在BO的延长线上时,第一种情况,当点M在DE边上时,由EMF∽△EDP求解,第二种情况,当点N在CE边上时,由△EFN∽△EOC求解;②当1≤t< ![]() 时和当
时和当 ![]() <t≤5时,分别求出S的取值范围,
<t≤5时,分别求出S的取值范围,
【考点精析】解答此题的关键在于理解相似三角形的应用的相关知识,掌握测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AD=8,E是边AB上一点,且AE=
 AB.⊙O经过点E,与边CD所在直线相切于点G(∠GEB为锐角),与边AB所在直线交于另一点F,且EG:EF=
AB.⊙O经过点E,与边CD所在直线相切于点G(∠GEB为锐角),与边AB所在直线交于另一点F,且EG:EF= 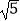 :2.当边AD或BC所在的直线与⊙O相切时,AB的长是 .
:2.当边AD或BC所在的直线与⊙O相切时,AB的长是 . 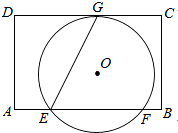
-
科目: 来源: 题型:
查看答案和解析>>【题目】勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪以灵感,他惊喜地发现,当两个全等的直角三角形如图1或图2摆放时,都可以用“面积法”来证明,下面是小聪利用图1证明勾股定理的过程:
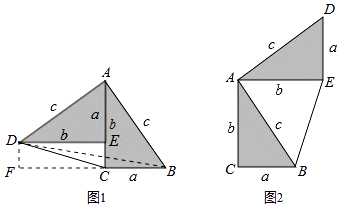
将两个全等的直角三角形按图1所示摆放,其中∠DAB=90°,求证:a2+b2=c2 .
证明:连结DB,过点D作BC边上的高DF,则DF=EC=b﹣a.
∵S四边形ADCB=S△ACD+S△ABC= b2+
b2+  ab.
ab.
又∵S四边形ADCB=S△ADB+S△DCB= c2+
c2+  a(b﹣a)
a(b﹣a)
∴ b2+
b2+  ab=
ab=  c2+
c2+  a(b﹣a)
a(b﹣a)
∴a2+b2=c2
请参照上述证法,利用图2完成下面的证明.
将两个全等的直角三角形按图2所示摆放,其中∠DAB=90°.
求证:a2+b2=c2
证明:连结
∵S五边形ACBED=
又∵S五边形ACBED=
∴
∴a2+b2=c2 . -
科目: 来源: 题型:
查看答案和解析>>【题目】八(1)班五位同学参加学校举办的数学素养竞赛.试卷中共有20道题,规定每题答对得5分,答错扣2分,未答得0分.赛后A,B,C,D,E五位同学对照评分标准回忆并记录了自己的答题情况(E同学只记得有7道题未答),具体如下表
参赛同学
答对题数
答错题数
未答题数
A
19
0
1
B
17
2
1
C
15
2
3
D
17
1
2
E
/
/
7
(1)根据以上信息,求A,B,C,D四位同学成绩的平均分;
(2)最后获知A,B,C,D,E五位同学成绩分别是95分,81分,64分,83分,58分. ①求E同学的答对题数和答错题数;
②经计算,A,B,C,D四位同学实际成绩的平均分是80.75分,与(1)中算得的平均分不相符,发现是其中一位同学记错了自己的答题情况,请指出哪位同学记错了,并写出他的实际答题情况(直接写出答案即可). -
科目: 来源: 题型:
查看答案和解析>>【题目】计算下列各题
(1)计算: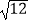 +2×(﹣5)+(﹣3)2+20140;
+2×(﹣5)+(﹣3)2+20140;
(2)化简:(a+1)2+2(1﹣a). -
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的袋中装有20个只有颜色不同的球,其中5个黄球,8个黑球,7个红球.
(1)求从袋中摸出一个球是黄球的概率;
(2)现从袋中取出若干个黑球,搅匀后,使从袋中摸出一个球是黑球的概率是 ,求从袋中取出黑球的个数.
,求从袋中取出黑球的个数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.

(1)求∠F的度数;
(2)若CD=2,求DF的长.
相关试题

