【题目】如图,已知A、B两点的坐标分别为(2,0)、(0,4),P是△AOB外接圆⊙C上的一点,且∠AOP=45°,则点P的坐标为 . 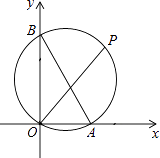
参考答案:
【答案】(3,3)
【解析】解:∵OB=4,OA=2, ∴AB= ![]() =2
=2 ![]() ,
,
∵∠AOP=45°,
∴P点横纵坐标相等,可设为a,即P(a,a),
∵∠AOB=90°,
∴AB是直径,
∴Rt△AOB外接圆的圆心为AB中点,坐标C(1,2),
P点在圆上,P点到圆心的距离为圆的半径 ![]() .
.
过点C作CF∥OA,过点P作PE⊥OA于E交CF于F,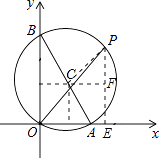
∴∠CFP=90°,
∴PF=a﹣2,CF=a﹣1,PC= ![]() ,
,
∴根据勾股定理得:(a﹣2)2+(a﹣1)2=( ![]() )2 ,
)2 ,
解得:a=3,
∴P(3,3);
所以答案是:(3,3).
【考点精析】解答此题的关键在于理解角平分线的性质定理的相关知识,掌握定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上,以及对圆心角、弧、弦的关系的理解,了解在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等;在同圆或等圆中,同弧等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用边长相等的下列两种正多边形,不能进行平面镶嵌的是( )
A. 等边三角形和正六边形 B. 正方形和正八边形
C. 正五边形和正十边形 D. 正六边形和正十二边形
-
科目: 来源: 题型:
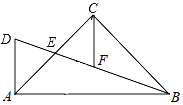
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的中点,AD⊥AB交BE延长线于点D,CF平分∠ACB交BD于点F,连接CD.
求证:(1)AD=CF;
(2)点F为BD的中点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,E,F分别为边AB,CD的中点,连接DE、BF、BD.

(1)求证:△ADE≌△CBF.
(2)若AD⊥BD,则四边形BFDE是什么特殊四边形?请证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在⊙O中,
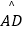 =
= 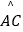 ,弦AB与弦AC交于点A,弦CD与AB交于点F,连接BC.
,弦AB与弦AC交于点A,弦CD与AB交于点F,连接BC. 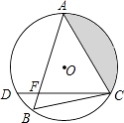
(1)求证:AC2=ABAF;
(2)若⊙O的半径长为2cm,∠B=60°,求图中阴影部分面积. -
科目: 来源: 题型:
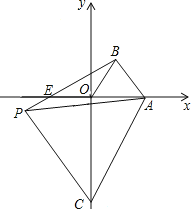
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A的坐标是(a,0)(a>0),点C是y轴上的一个动点,点C在y轴上移动时,始终保持△ACP是等边三角形,当点C移动到点O时,得到等边△AOB(此时点P与点B重合).
(1)点C在移动的过程中,当等边三角形ACP的顶点P在第三象限时(如图所示),求证:△AOC≌△ABP;
(2)若点P在第三象限,BP交x轴于点E,且∠ACO=20°,求∠PAE的度数和E点的坐标;
(3)若∠APB=30°,则点P的横坐标为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在正方形ABCD中,E、F分别是边AD、DC上的点,且AF⊥BE.
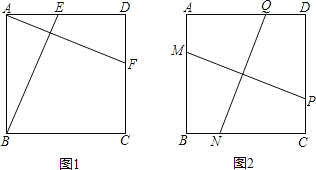
(1)求证:AF=BE;
(2)如图2,在正方形ABCD中,M、N、P、Q分别是边AB、BC、CD、DA上的点,且MP⊥NQ.MP与NQ是否相等?并说明理由.
相关试题

