【题目】如图,正方形ABCD的边长为10 cm,点E,F,G,H分别从点A,B,C,D出发,以2 cm/s的速度同时分别向点B,C,D,A运动.
(1)在运动的过程中,四边形EFGH是何种四边形?请说明理由.
(2)运动多少秒后,四边形EFGH的面积为52cm2?
参考答案:
【答案】(1)见解析;(2)运动2s或3s后,四边形EFGH的面积为52cm2.
【解析】试题分析:
试题解析:解:(1)四边形EFGH为正方形.理由如下:
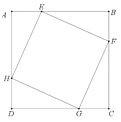
设运动时间为t s,则AE=BF=CG=DH=2tcm,
在正方形ABCD中,∠A=∠B=∠C=∠D=90°,
AB=BC=CD=DA,∴BE=CF=DG=AH.
在△AEH和△BFE中, 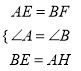 ,
,
∴△AEH≌△BFE,
同理可证:△AEH≌△BFE≌△CGF≌△DHG,∴EH=FE=GF=HG,
∴四边形EFGH为菱形.
∵△AEH≌△BFE,
∴∠AEH=∠BFE,而∠BFE+∠BEF=90°,
∴∠AEH+∠BEF=90°,
∴∠HEF=90°,
∴四边形EFGH为正方形.
(2)设运动的时间为x s,则AE=BF=CG=DH=2xcm.
∵AB=BC=CD=DA=10cm,
∴BE=CF=DG=AH=(10-2x)cm.
由勾股定理得S四边形EFGH=EH2=AE2+AH2=(2x)2+(10-2x)2=8x2-40x+100.
当S四边形EFGH=52 cm2时,8x2-40x+100=52,即x2-5x+6=0,
解得x1=2,x2=3.当x=2时,AE=2x=2×2=4<10;
当x=3时,AE=2x=2×3=6<10.
∴x=2或3均符合题意.故运动2s或3s后,四边形EFGH的面积为52cm2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上,与表示数-1的点的距离是5的点表示的数是( )
A. 4 B. —6 C. ±3 D. 4或-6
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC=90°,以AB为直径的⊙O与AC边交于点D,过点D的直线交BC边于点E,∠BDE=∠A.
(1)判断直线DE与⊙O的位置关系,并说明理由;
(2)若⊙O的半径R=5,cosA=
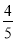 ,求线段CD的长.
,求线段CD的长.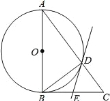
-
科目: 来源: 题型:
查看答案和解析>>【题目】把199 000 000用科学记数法写成1.99×10n-3的形式,求n的值
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形的一个内角为70°,它的一腰上的高与底边所夹的角的度数是( )
A. 35° B. 20° C. 35°或20° D. 无法确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市语委办为了解本市八年级学生汉字书写能力情况,随机抽查了部分八年级学生,并将调查数据进行如下整理,请解答以下问题:
正确书写出的字数x(个)
频数(人)
频率
0≤x≤5
8
0.16
5<x≤10
10<x≤15
16
0.32
15<x≤20
8
0.16
20<x≤25
4
0.08
25<x≤30
2
0.04
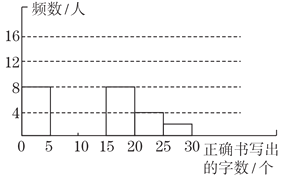
(1)把频数、频率分布表和频数分布直方图补充完整;
(2)根据统计图,可知“正确书写的字数”的中位数应处的范围是________;
(3)若正确书写的字数不超过15个为不及格,请求出不及格人数占所抽查人数的百分比;并根据调查数据估计,该市20 000名八年级学生中,有多少名学生不及格?对此,请你用一句话谈谈你的建议或感想.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了保护环境,某开发区综合治理指挥部决定购买A,B两种型号的污水处理设备共10台.已知用90万元购买A型号的污水处理设备的台数与用75万元购买B型号的污水处理设备的台数相同,每台设备价格及月处理污水量如下表所示:
污水处理设备
A型
B型
价格(万元/台)
m
m﹣3
月处理污水量(吨/台)
220
180
(1)求m的值;
(2)由于受资金限制,指挥部用于购买污水处理设备的资金不超过165万元,问有多少种购买方案?并求出每月最多处理污水量的吨数.
相关试题

