【题目】如图1,在平面直角坐标系中,点A,B,C的坐标分别是(0,a),(b,0),(a,﹣b)且a2+b2+4a﹣4b=﹣8,连接BC交y轴于点M,N为AC中点,连接NO并延长至D,使OD=ON,连接BD.
(1)求a,b的值;
(2)求∠DBC;
(3)如图2,Q为ON,BC的交点,连接AQ,AB,过点O作OP⊥OQ,交AB于P,过点O作OH⊥AB于H,交BQ于E,请探究线段EH,PH与OH之间有何数量关系?并证明你的结论.
参考答案:
【答案】解:(1)∵点A,B,C的坐标分别是(0,a),(b,0),(a,﹣b)且a2+b2+4a﹣4b=﹣8,
∴(a+2)2+(b﹣2)2=0,
∴a+2=0,b﹣2=0,
∴a=﹣2,b=2;
(2)∵A(0,﹣2),B(2,0),C(﹣2,﹣2),
∴AC∥x轴,
∵N为AC中点,
∴N(﹣1,﹣2),
∴AN=1,
∵OD=ON,
∴D和N点关于O点对称,
∴D(1,2),
设直线BD的解析式为y=k1x+b1 ,
∴![]() ,解得k1=﹣2,
,解得k1=﹣2,
设直线BC的解析式为y=k2x+b2 ,
∴![]() ,解得
,解得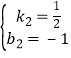 ,
,
∵k1k2=﹣1,
∴DB⊥BC,
∴∠DBC=90°;
(3)∵A(0,﹣2),B(2,0),
∴OA=OB=2,
∵OH⊥AB,
∴AH=BH,
∴H(1,﹣1),
∴直线OH:y=﹣x,OH=![]() ,
,
∵线BC的解析式为y=![]() x﹣1,
x﹣1,
解 得
得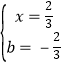 ,
,
∴E(![]() ,﹣
,﹣![]() ),
),
∴EH=![]() =
=![]() ,
,
∵N(﹣1,﹣2),
∴直线ON:y=2x,
∵OP⊥OQ,
∴直线OP:y=﹣![]() x,
x,
解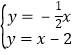 得
得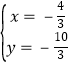 ,
,
∴P(![]() ,﹣
,﹣![]() ),
),
∴PH=![]() =
=![]() ,
,
∴OH﹣EH=2OH;
【解析】(1)把a2+b2+4a﹣4b=﹣8化成(a+2)2+(b﹣2)2=0,根据非负数的和等于0,即可求得a,b的值;
(2)根据A(0,﹣2),B(2,0),C(﹣2,﹣2),对称AC∥x轴,从而求得N的坐标,根据中心对称的性质对称D的坐标,然后根据待定系数法求得直线BD的斜率和直线BC的斜率,即可判定两条直线垂直,从而求得∠DBC=90°;
(3)分别求得E,H,P的坐标,根据勾股定理求得线段EH、OH、OH的长,即可得出线段EH,PH与OH之间的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:﹣2xy2+8xy﹣8x= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.﹣a(a﹣b)=﹣a2﹣ab
B.(2ab)2÷a2b=4ab
C.2ab3a=6a2b
D.(a﹣1)(1﹣a)=a2﹣1 -
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)(+3.5)﹣1.4﹣(2.5)+(﹣4.6)
(2)[2﹣5×(﹣ ) 2]÷(﹣
) 2]÷(﹣  )
)
(3)[2 ﹣(
﹣(  +
+  ﹣
﹣  )×24]÷5×(﹣1)2009
)×24]÷5×(﹣1)2009
(4)﹣22+|5﹣8|+24÷(﹣3)×
(5)(xy2﹣x2y)﹣2( xy+xy2)+3x2y
(6)5a2﹣[a2+(5a2﹣2a)﹣2(a2﹣3a)]. -
科目: 来源: 题型:
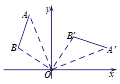
查看答案和解析>>【题目】如图,将线段AB绕点O顺时针旋转90°得到线段A′B′,那么A(﹣2,5)的对应点A′的坐标是
A. (2,5) B. (5,2) C. (4,
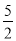 ) D. (
) D. (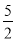 ,4)
,4) -
科目: 来源: 题型:
查看答案和解析>>【题目】方程x+5=2x﹣3的解是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】商店为了对某种商品促销,将定价为3元的商品以下列方式优惠销售:若购买不超过5件,则按原价付款;若一次性购买5件以上,则超过部分打八折.那么用27元钱最多可以购买该商品________件.
相关试题

