Question

【题目】如图，在边长为12的正方形ABCD中，E是边CD的中点，将△ADE沿AE对折至△AFE，延长EF交BC于点G．则BG的长为（ ）
A.5
B.4
C.3
D.2

Answer 1

【答案】B
【解析】解：在正方形ABCD中，AD=AB=BC=CD，∠D=∠B=∠BCD=90°， ∵将△ADE沿AE对折至△AFE，
∴AD=AF，DE=EF，∠D=∠AFE=90°，
∴AB=AF，∠B=∠AFG=90°，
又∵AG=AG，
在Rt△ABG和Rt△AFG中，
，
∴Rt△ABG≌Rt△AFG（HL），
∴BG=GF，
∵E是边CD的中点，
∴DE=CE=6，
设BG=x，则CG=12﹣x，GE=x+6，
∵GE2=CG2+CE2
∴（x+6）2=（12﹣x）2+62 ，
解得 x=4
∴BG=4．
故选B．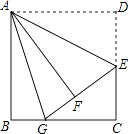

【考点精析】根据题目的已知条件，利用翻折变换（折叠问题）的相关知识可以得到问题的答案，需要掌握折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等．