Question

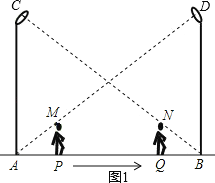
【题目】如图，小华在晚上由路灯A走向路灯B．当他走到点P时，发现他身后影子的顶部刚好接触到路灯A的底部；当他向前再步行12m到达点Q时，发现他身前影子的顶部刚好接触到路灯B的底部．已知小华的身高是1.6m，两个路灯的高度都是9.6m，且AP=QB．

（1）求两个路灯之间的距离．

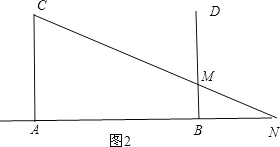
（2）当小华走到路灯B的底部时，他在路灯A下的影长是多少？

Answer 1

【答案】（1）18m；（2）3.6m

【解析】

试题分析：（1）如图1，先证明△APM∽△ABD，利用相似比可得AP=AB，再证明△BQN∽△BAC，利用相似比可得BQ=AB，则AB+12+AB=AB，解得AB=18（m）；

（2）如图1，他在路灯A下的影子为BN，证明△NBM∽△NAC，利用相似三角形的性质得=，然后利用比例性质求出BN即可．

解：（1）如图1，

∵PM∥BD，

∴△APM∽△ABD，

=，即=，

∴AP=AB，

∵NQ∥AC，

∴△BNQ∽△BCA，

∴=，即=，

∴BQ=AB，

而AP+PQ+BQ=AB，

∴AB+12+AB=AB，

∴AB=18．

答：两路灯的距离为18m；

（2）如图2，他在路灯A下的影子为BN，

∵BM∥AC，

∴△NBM∽△NAC，

∴=，即=，解得BN=3.6．

答：当他走到路灯B时，他在路灯A下的影长是3.6m．