【题目】已知抛物线y=x2﹣2x﹣3与x轴交于A,B两点,点A在点B的左侧.
(1)求A,B两点的坐标和此抛物线的对称轴;
(2)设此抛物线的顶点为C,点D与点C关于x轴对称,求四边形ACBD的面积.
参考答案:
【答案】(1)点A的坐标是(﹣1,0),B的坐标是(3,0).(2)线对称轴是x=1;
(3)∴四边形ACBD的面积是:16.
【解析】
试题分析:(1)令y=0解方程即可求得A和B的横坐标,然后利用配方法即可求得对称轴和顶点坐标;
(2)首先求得D的坐标,然后利用面积公式即可求解.
试题解析:(1)令y=0,则x2﹣2x﹣3=0,解得:x1=﹣1,x2=3.
∵点A在点B的左侧.∴点A的坐标是(﹣1,0),B的坐标是(3,0).
∵y=﹣x2﹣2x﹣3=(x﹣1)2﹣4,∴抛物线对称轴是x=1;
(2)∵顶点C的坐标是(1,﹣4),D与点C关于x轴对称,
∴D的坐标是(1,4).∴AB=3﹣(﹣1)=4,CD=4﹣(﹣4)=8,
∴四边形ACBD的面积是:![]() ABCD=
ABCD=![]() ×4×8=16.
×4×8=16.
-
科目: 来源: 题型:
查看答案和解析>>【题目】《九章算术》是中国传统数学重要的著作,奠定了中国传统数学的基本框架.《九章算术》中记载:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,间径几何?”(如图①)

阅读完这段文字后,小智画出了一个圆柱截面示意图(如图②),其中BO⊥CD于点A,求间径就是要求⊙O的直径.
再次阅读后,发现AB= 寸,CD= 寸(一尺等于十寸),通过运用有关知识即可解决这个问题.请你补全题目条件,并帮助小智求出⊙O的直径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列各式:12+1=1×2,22+2=2×3,32+3=3×4,…请你将猜想得到的规律用自然数n表示出来: .
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
如图1,在平面直角坐标系xOy中,直线y1=ax+b与双曲线y2=
 交于A(1,3)和B(﹣3,﹣1)两点.
交于A(1,3)和B(﹣3,﹣1)两点.观察图象可知:
①当x=﹣3或1时,y1=y2;
②当﹣3<x<0或x>1时,y1>y2,即通过观察函数的图象,可以得到不等式ax+b>
 的解集.
的解集.有这样一个问题:求不等式x3+4x2﹣x﹣4>0的解集.
某同学根据学习以上知识的经验,对求不等式x3+4x2﹣x﹣4>0的解集进行了探究.

下面是他的探究过程,请将(2)、(3)、(4)补充完整:
(1)将不等式按条件进行转化:
当x=0时,原不等式不成立;
当x>0时,原不等式可以转化为x2+4x﹣1>
 ;
;当x<0时,原不等式可以转化为x2+4x﹣1<
 ;
;(2)构造函数,画出图象
设y3=x2+4x﹣1,y4=
 ,在同一坐标系中分别画出这两个函数的图象.
,在同一坐标系中分别画出这两个函数的图象.双曲线y4=
 如图2所示,请在此坐标系中画出抛物线y3=x2+4x﹣1;(不用列表)
如图2所示,请在此坐标系中画出抛物线y3=x2+4x﹣1;(不用列表)(3)确定两个函数图象公共点的横坐标
观察所画两个函数的图象,猜想并通过代入函数解析式验证可知:满足y3=y4的所有x的值为 ;
(4)借助图象,写出解集
结合(1)的讨论结果,观察两个函数的图象可知:不等式x3+4x2﹣x﹣4>0的解集为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次体育达标测试中,九年级(3)班的15名男同学的引体向上成绩如下表所示:
成绩(个)
8
9
11
12
13
15
人数
1
2
3
4
3
2
这15名男同学引体向上成绩的中位数和众数分别是( )
A.12,13
B.12,12
C.11,12
D.3,4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC的斜边BC上截取CD=CA,过点D作DE⊥BC,交AB于E,则下列结论一定正确的是( )
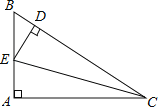
A. AE=BE B. DB=DE C. AE=BD D. ∠BCE=∠ACE
-
科目: 来源: 题型:
查看答案和解析>>【题目】青藏高原是世界上海拔最高的高原,它的面积约为2500000平方千米.将2500000用科学记数法表示应为( )
A.0.25×107
B.2.5×107
C.2.5×106
D.25×105
相关试题

