Question

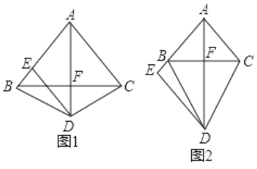
【题目】如图1，已知△ABC中，AB=AC，点D是△ABC外一点(与点A分别在直线BC两侧).且DB=DC，过点D作DE//AC，交射线AB于E，连接AD交BC于F.

(1)求证：AD垂直BC；

(2)如图1，点E在线段AB上且不与B重合时，求证：DE=AE；

(3)如图2，当点E在线段AB的延长线上时，请直接写出线段DE，AC，BE的数量关系.

Answer 1

【答案】（1）详见解析；（2）详见解析；（3）DE=AC+BE

【解析】

（1）根据线段垂直平分线的判定定理即可得到结论；
（2）根据等腰三角形的性质得到∠BAF=∠CAF，根据平行线的性质得到∠CAF=∠ADE，等量代换得到∠BAF=∠ADE，于是得到DE=AE；

（3）由（1）得AF⊥BC，根据等腰三角形的性质得到∠BAF=∠CAE，根据平行线的性质得到∠EDA=∠CAF，等量代换得到∠BAF=∠EDA于是得到结论．

(1)∵AB=AC

∴点A在线段BC的垂直平分线上，

∵DB=DC

∴点D在线段BC的垂直平分线上，

∴直线AD是BC的垂直平分线，

∴AD垂直BC；

(2)∵AB=AC，AD⊥BC

∴∠BAD=∠CAD

∵DE∥AC

∴∠EDA=∠CAD

∴∠BAD=∠EDA

∴DE=AE

(3) DE=BE+AC，

由（1）得AF⊥BC，

∵AB=AC，

∴∠BAF=∠CAF，

∵DE∥AC，

∴∠EDA=∠CAF，

∴∠BAF=∠EDA，

∴EA=ED，

∵EA=EB+BA=EB+AC，

∴DE=BE+AC．