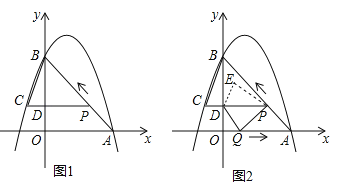
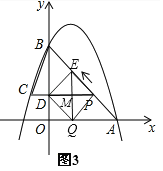
【题目】如图 1,二次函数![]() 的图像过点 A (3,0),B (0,4)两点,动点 P 从 A 出发,在线段 AB 上沿 A → B 的方向以每秒 2 个单位长度的速度运动,过点P作 PD⊥y 于点 D ,交抛物线于点 C .设运动时间为 t (秒).
的图像过点 A (3,0),B (0,4)两点,动点 P 从 A 出发,在线段 AB 上沿 A → B 的方向以每秒 2 个单位长度的速度运动,过点P作 PD⊥y 于点 D ,交抛物线于点 C .设运动时间为 t (秒).
(1)求二次函数![]() 的表达式;
的表达式;
(2)连接 BC ,当t=![]() 时,求△BCP的面积;
时,求△BCP的面积;
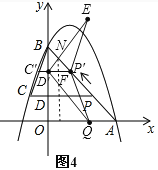
(3)如图 2,动点 P 从 A 出发时,动点 Q 同时从 O 出发,在线段 OA 上沿 O→A 的方向以 1个单位长度的速度运动,当点 P 与 B 重合时,P 、 Q 两点同时停止运动,连接 DQ 、 PQ ,将△DPQ沿直线 PC 折叠到 △DPE .在运动过程中,设 △DPE 和 △OAB重合部分的面积为 S ,直接写出 S 与 t 的函数关系式及 t 的取值范围.
参考答案:
【答案】(1)![]() ;(2)4;(3)
;(2)4;(3)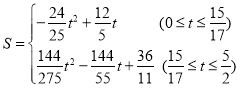 .
.
【解析】
试题分析:(1)直接将A、B两点的坐标代入列方程组解出即可;
(2)如图1,要想求△BCP的面积,必须求对应的底和高,即PC和BD;先求OD,再求BD,PC是利用点P和点C的横坐标求出,要注意符号;
(3)分两种情况讨论:①△DPE完全在△OAB中时,即当![]() 时,如图2所示,重合部分的面积为S就是△DPE的面积;②△DPE有一部分在△OAB中时,当
时,如图2所示,重合部分的面积为S就是△DPE的面积;②△DPE有一部分在△OAB中时,当![]() 时,如图4所示,△PDN就是重合部分的面积S.
时,如图4所示,△PDN就是重合部分的面积S.
试题解析:(1)把A(3,0),B(0,4)代入![]() 中得:
中得:
![]() ,解得:
,解得:![]() ,∴解析式为:
,∴解析式为:![]() ;
;
(2)如图1,当![]() 时,AP=2t,∵PC∥x轴,∴
时,AP=2t,∵PC∥x轴,∴![]() ,∴
,∴![]() ,∴OD=
,∴OD=![]() =
=![]() =
=![]() ,当y=
,当y=![]() 时,
时,![]() =
=![]() ,
,![]() ,解得:
,解得:![]() ,
,![]() ,∴C(﹣1,
,∴C(﹣1,![]() ),由
),由![]() ,得
,得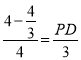 ,则PD=2,∴S△BCP=
,则PD=2,∴S△BCP=![]() ×PC×BD=
×PC×BD=![]() =4;
=4;
(3)分两种情况讨论:①如图3,当点E在AB上时,由(2)得OD=QM=ME=![]() ,∴EQ=
,∴EQ=![]() ,由折叠得:EQ⊥PD,则EQ∥y轴,∴
,由折叠得:EQ⊥PD,则EQ∥y轴,∴![]() ,∴
,∴ ,∴t=
,∴t=![]() ,同理得:PD=
,同理得:PD=![]() ,∴当
,∴当![]() 时,S=S△PDQ=
时,S=S△PDQ=![]() ×PD×MQ=
×PD×MQ=![]() ,
,![]() ;
;
②当![]() 时,如图4,P′D′=
时,如图4,P′D′=![]() ,点Q与点E关于直线P′C′对称,则Q(t,0)、E(t,
,点Q与点E关于直线P′C′对称,则Q(t,0)、E(t,![]() ),∵AB的解析式为:
),∵AB的解析式为:![]() ,D′E的解析式为:
,D′E的解析式为:![]() ,则交点N(
,则交点N(![]() ,
,![]() ),∴S=S△P′D′N=
),∴S=S△P′D′N=![]() ×P′D′×FN=
×P′D′×FN=![]() ,∴
,∴![]() .
.
综上所述: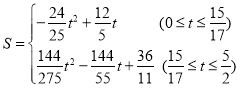 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算中,正确的是( )
A.a6÷a3=a2B.a2a3=a6C.(a2)3=a6D.3a3﹣2a2=a
-
科目: 来源: 题型:
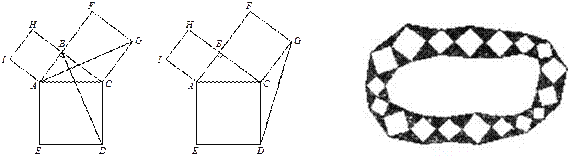
查看答案和解析>>【题目】如图,在△ABC中,∠ABC=90°,分别以边AB、BC、CA向△ABC外作正方形ABHI、正方形BCGF、正方形CAED,连接GD,AG,BD. (提示:正方形的四条边相等,四个角均为直角,可直接运用。)
(1)如图1,求证:AG=BD.
(2)如图2,试说明:S△ABC=S△CDG.
(3)园林小路,曲径通幽,如图3所示,小路由白色的正方形大理石和黑色的三角形大理石铺成,已知中间的所有正方形的面积之和是a平方米,内圈的所有三角形的面积之和是b平方米,这条小路一共占地 平方米.(不用写过程)
-
科目: 来源: 题型:
查看答案和解析>>【题目】商家花费1440元购进某种水果80千克,销售中有10%的水果正常损耗,为了避免亏本,售价至少应定为________元/千克.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果将抛物线y=(x﹣2)2+1向左平移1个单位,再向上平移3个单位,那么所得新抛物线的解析式为( )
A.y=(x﹣3)2+4B.y=(x﹣1)2+4C.y=(x+1)2+2D.y=(x+1)2
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校举行“纪念反法西斯战争胜利70周年”演讲比赛,共有15名同学进入决赛,比赛将评出金奖1名,银奖3名,铜奖4名.某参赛选手知道自己的分数后,要判断自己能否获奖,他应该关注的是有关成绩的 . (填“平均数”、“中位数”或“众数”)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司今年如果用原线下销售方式销售一产品,每月的销售额可达100万元.由于该产品供不应求,公司计划于3月份开始全部改为线上销售,这样,预计今年每月的销售额y(万元)与月份x(月)之间的函数关系的图象如图1中的点状图所示(5月及以后每月的销售额都相同),而经销成本p(万元)与销售额y(万元)之间函数关系的图象图2中线段AB所示.

(1)求经销成本p(万元)与销售额y(万元)之间的函数关系式;
(2)分别求该公司3月,4月的利润;
(3)问:把3月作为第一个月开始往后算,最早到第几个月止,该公司改用线上销售后所获得利润总额比同期用线下方式销售所能获得的利润总额至少多出200万元?(利润=销售额﹣经销成本)
相关试题

