【题目】如图,在矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,且OE=OD,则AP的长为 ( ) .

A.4.8B.3![]() C.5D.3
C.5D.3![]()
参考答案:
【答案】A
【解析】
由折叠的性质得出EP=AP,∠E=∠A=90°,BE=AB=8,由ASA证明△ODP≌△OEG,得出OP=OG,PD=GE,设AP=EP=x,则PD=GE=6x,DG=x,求出CG、BG,根据勾股定理得出方程,解方程即可.
解:如图所示,设BE与CD交于点G,

∵四边形ABCD是矩形,
∴∠D=∠A=∠C=90°,AD=BC=6,CD=AB=8,
根据题意得:△ABP≌△EBP,
∴EP=AP,∠E=∠A=90°,BE=AB=8,
在△ODP和△OEG中,
∠D=∠E,OD=OE,∠DOP=∠EOG,
∴△ODP≌△OEG(ASA),
∴OP=OG,PD=GE,
∴DG=EP,
设AP=EP=x,则PD=GE=6x,DG=x,
∴CG=8x,BG=8(6x)=2+x,
根据勾股定理得:BC2+CG2=BG2,
即62+(8x)2=(x+2)2,
解得:x=4.8,
∴AP=4.8,
故选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一笔直的海岸线
 上有
上有 、
、 两个观测站,
两个观测站, 在
在 的正东方向,
的正东方向, (单位:
(单位: )有一艘小船在点
)有一艘小船在点 处,从
处,从 测得小船在北偏西
测得小船在北偏西 的方向,从
的方向,从 测得小船在北偏东
测得小船在北偏东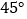 的方向.(结果保留根号)
的方向.(结果保留根号)(1)求点
 到海岸线
到海岸线 的距离;
的距离;(2)小船从点
 处沿射线
处沿射线 的方向航行一段时间后,到达点
的方向航行一段时间后,到达点 处,此时,从
处,此时,从 测得小船在北偏西
测得小船在北偏西 的方向,求点
的方向,求点 与点
与点 之间的距离.
之间的距离.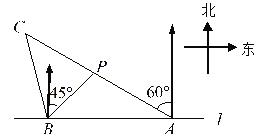
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)

(2)(2a3b-4ab3)·(-
 ab)-(-2a2)2(-b2)
ab)-(-2a2)2(-b2)(3)先化简,再求代数式(a+2b)(a-2b)+(a+2b)2-4ab 的值,其中 a=1,b=

-
科目: 来源: 题型:
查看答案和解析>>【题目】二元一次方程组
 的解 x,y 的值是一个等腰三角形两边的长,且这个等腰三角形的周长为 5,求腰的长.(注:等腰三角形中相等的两条边叫做等腰三角形的腰)
的解 x,y 的值是一个等腰三角形两边的长,且这个等腰三角形的周长为 5,求腰的长.(注:等腰三角形中相等的两条边叫做等腰三角形的腰) -
科目: 来源: 题型:
查看答案和解析>>【题目】某博物馆每周都吸引大量中外游客前来参观,如果游客过多,对馆中的珍贵文物会产生不利影响,但同时考虑到文物的修缮和保存费用问题,还要保证一定的门票收入,因此,博物馆采取了涨浮门票价格的方法来控制参观人数,在该方法实施过程中发现:每周参观人数与票价之间存在着如图所示的一次函数关系.在这种情况下,如果要保证每周
 万元的门票收入,那么每周应限定参观人数是多少?门票价格应是多少.
万元的门票收入,那么每周应限定参观人数是多少?门票价格应是多少.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某化妆品店老板到厂家选购A、B两种品牌的化妆品,若购进A品牌的化妆品5套,B品牌的化妆品6套,需要950元;若购进A品牌的化妆品3套,B品牌的化妆品2套,需要450元.
 求A、B两种品牌的化妆品每套进价分别为多少元?
求A、B两种品牌的化妆品每套进价分别为多少元? 若销售1套A品牌的化妆品可获利30元,销售1套B品牌的化妆品可获利20元,根据市场需求,化妆品店老板决定,购进B品牌化妆品的数量比购进A品牌化妆品数量的2倍还多4套,且B品牌化妆品最多可购进40套,这样化妆品全部售出后,可使总的获利不少于1200元,问有几种进货方案?如何进货?
若销售1套A品牌的化妆品可获利30元,销售1套B品牌的化妆品可获利20元,根据市场需求,化妆品店老板决定,购进B品牌化妆品的数量比购进A品牌化妆品数量的2倍还多4套,且B品牌化妆品最多可购进40套,这样化妆品全部售出后,可使总的获利不少于1200元,问有几种进货方案?如何进货? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD中,E、F分别是AB、DC边上的点,且AE=CF,
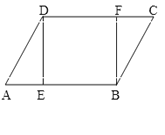
(1)求证:
 ≌
≌ .
.(2)若
 DEB=90
DEB=90 ,求证四边形DEBF是矩形.
,求证四边形DEBF是矩形.
相关试题

