【题目】如图,在△ABC中,AB=BC,点E在边AB上,EF⊥AC于F.

(1)尺规作图:过点A作AD⊥BC于点D(保留作图痕迹,不写作法);(2)求证:∠CAD=∠AEF;(3)若∠ABC=45°,AD与EF交于点G,求证:EG=2AF.
参考答案:
【答案】(1)图形见解析;(2)证明过程见解析;(3)证明过程见解析
【解析】
试题分析:(1)、根据高线的作法作出图形;(2)、根据AB=BC得出∠C=∠BAC,根据垂直得出∠CDA=∠EFA=90°,根据三角形内角和定理得出∠DAC=∠AEF;(3)、过点E作EM∥BC,题意得出EGN≌△ANM,从而说明EG=AM,根据等腰三角形的三线合一定理得出AM=2AF,则EG=2AF.
试题解析:(1)、作图略
(2)、∵BC=BA ∴∠C=∠BAC ∵AD⊥BC,EF⊥AC ∴∠CDA=∠EFA=900
∴1800-∠C -∠CDA=1800-∠BAC -∠EFA 即∠DAC=∠AEF
(3)、过点E作EM∥BC分别交AD、AC于点N、M

∵EM∥BC ∴∠MEA=∠B=450,∠ENA=∠ADB=900, ∴△AEN为等腰直角三角形,∠ANM=900,
∴NE=NA ∴∠ENA=∠ANM ∵EF⊥AC, ∴∠EFA=900 ∴∠ENA=∠EFA
又∵∠EGN=∠AGF ∴1800-∠ENA -∠EGN=1800-∠EFA -∠AGF 即∠NEG=∠NAM
∴△ENG≌△ANM ∴EG=AM ∵BC=BA ∴∠C=∠BAC
∵EM∥BC ∴∠EMA=∠C ∴∠EMA=∠BAC ∴△EMA为等腰三角形
又 ∵EF⊥MA ∴AM=2AF ∴EG=2AF
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个正多边形的一个外角等于 40°,则这个多边形是______边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a=﹣a,则a=( )
A.1
B.﹣1
C.0
D.1或﹣1 -
科目: 来源: 题型:
查看答案和解析>>【题目】某市举行“行动起来,对抗雾霾”为主题的植树活动,某街道积极响应,决定对该街道进行绿化改造,共购进甲、乙两种树共500棵,已知甲树每棵800元,乙树每棵1200元.
(1)若购买两种树总金额为560000元,求甲、乙两种树各购买了多少棵?
(2)若购买甲树的金额不少于购买乙树的金额,至少应购买甲树多少棵?
-
科目: 来源: 题型:
查看答案和解析>>【题目】桂林市某气象站测得六月份一周七天的降雨量分别为0,32,11,45,8,51,27(单位:mm),这组数据的极差是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.2a+5b=7ab
B.2ab﹣ba=ab
C.﹣5x2+2x2=﹣3
D.﹣(a﹣b)=b+a -
科目: 来源: 题型:
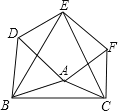
查看答案和解析>>【题目】如图,已知△ABC,分别以它的三边为边长,在BC边的同侧作三个等边三角形,即△ABD,△BCE,△ACF,求证:四边形ADEF是平行四边形。
相关试题

