【题目】已知Rt△ABC中,∠ACB=90°,CA=CB=4,另有一块等腰直角三角板的直角顶点放在C处,CP=CQ=2,将三角板CPQ绕点C旋转(保持点P在△ABC内部),连接AP、BP、BQ.
(1)如图1求证:AP=BQ;
(2)如图2当三角板CPQ绕点C旋转到点A、P、Q在同一直线时,求AP的长;
(3)设射线AP与射线BQ相交于点E,连接EC,写出旋转过程中EP、EQ、EC之间的数量关系.

参考答案:
【答案】(1)证明见解析(2)![]() (3)EP+EQ=
(3)EP+EQ= ![]() EC
EC
【解析】
(1)由题意可得:∠ACP=∠BCQ,即可证△ACP≌△BCQ,可得 AP=CQ;
作 CH⊥PQ 于 H,由题意可求 PQ=2![]() ,可得 CH=
,可得 CH=![]() ,根据勾股定理可求
,根据勾股定理可求
AH=![]() ,即可求 AP 的长;
,即可求 AP 的长;
作 CM⊥BQ 于 M,CN⊥EP 于 N,设 BC 交 AE 于 O,由题意可证△CNP≌△ CMQ,可得 CN=CM,QM=PN,即可证 Rt△CEM≌Rt△CEN,EN=EM,∠CEM=
∠CEN=45°,则可求得 EP、EQ、EC 之间的数量关系.
解:(1)如图 1 中,∵∠ACB=∠PCQ=90°,
∴∠ACP=∠BCQ 且 AC=BC,CP=CQ
∴△ACP≌△BCQ(SAS)
∴PA=BQ
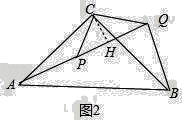 如图 2 中,作 CH⊥PQ 于 H
如图 2 中,作 CH⊥PQ 于 H
∵A、P、Q 共线,PC=2,
∴PQ=2![]() ,
,
∵PC=CQ,CH⊥PQ
∴CH=PH= ![]()
在 Rt△ACH 中,AH=![]() =
= ![]()
∴PA=AH﹣PH= ![]() -
-![]()
解:结论:EP+EQ=![]() EC
EC
理由:如图 3 中,作 CM⊥BQ 于 M,CN⊥EP 于 N,设 BC 交 AE 于 O.
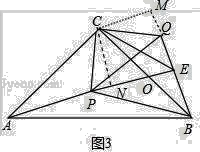
∵△ACP≌△BCQ,
∴∠CAO=∠OBE,
∵∠AOC=∠BOE,
∴∠OEB=∠ACO=90°,
∵∠M=∠CNE=∠MEN=90°,
∴∠MCN=∠PCQ=90°,
∴∠PCN=∠QCM,
∵PC=CQ,∠CNP=∠M=90°,
∴△CNP≌△CMQ(AAS),
∴CN=CM,QM=PN,
∴CE=CE,
∴Rt△CEM≌Rt△CEN(HL),
∴EN=EM,∠CEM=∠CEN=45°
∴EP+EQ=EN+PN+EM﹣MQ=2EN,EC=![]() EN,
EN,
∴EP+EQ=![]() EC
EC
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,直线
 与抛物线
与抛物线 交于不同的两点
交于不同的两点 、
、 (点
(点 在点
在点 的左侧).
的左侧).(1)直接写出
 的坐标 ; (用
的坐标 ; (用 的代数式表示)
的代数式表示)(2)设抛物线的顶点为
 ,对称轴
,对称轴 与直线
与直线 的交点为
的交点为 ,连结
,连结 、
、 ,若S△NDC=3×S△MDC,求抛物线的解析式;
,若S△NDC=3×S△MDC,求抛物线的解析式;(3)如图②,在(2)的条件下,设该抛物线与
 轴交于
轴交于 、
、 两点,点
两点,点 为直线
为直线 下方抛物线上一动点,连接
下方抛物线上一动点,连接 、
、 ,设直线
,设直线 交线段
交线段 于点
于点 ,△MPQ的面积为
,△MPQ的面积为 ,△MAQ的面积为
,△MAQ的面积为 ,求
,求 的最大值.
的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市预测某饮料有发展前途,用1600元购进一批饮料,面市后果然供不应求,又用6000元购进这批饮料,第二批饮料的数量是第一批的3倍,但单价比第一批贵2元.
(1)第一批饮料进货单价多少元?
(2)若二次购进饮料按同一价格销售,两批全部售完后,获利不少于1200元,那么销售单价至少为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在扇形OAB中,∠AOB=110°,半径OA=18,将扇形OAB沿过点B的直线折叠,点O恰好落在弧AB上的点D处,折痕交OA于点C,则弧AD的长为( )
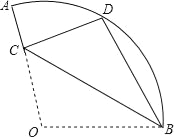
A. 2π B. 3π C. 4π D. 5π
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图甲,对于平面上不大于90°的∠MON,我们给出如下定义:如果点P在∠MON的内部,作PE⊥OM,PF⊥ON,垂足分别为点E、F,那么称PE+PF的值为点P相对于∠MON的“点角距离”,记为d(P,∠MON).如图乙,在平面直角坐标系xOy中,点P在坐标平面内,且点P的横坐标比纵坐标大2,对于∠xOy,满足d(P,∠xOy)=10,点P的坐标是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l1与l2相交,且夹角为45°,点P在角的内部,小明用下面的方法作点P的对称点:先以l1为对称轴作点P关于l1的对称点P1,再以l2为对称轴作点P1关于l2的对称点P2,然后再以l1为对称轴作点P2关于l1的对称点P3,以l2为对称轴作点P3关于l2的对称点P4,...,如此继续,得到一系列的点P1,P2,...,Pn,若点Pn与点P重合,则n的值可以是( )

A.2019B.2018C.2017D.2016
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为4的正方形ABCD内接于⊙O,点E是弧AB上的一动点(不与点A、B重合),点F是弧BC上的一点,连接OE,OF,分别与交AB,BC于点G,H,且∠EOF=90°,连接GH,有下列结论:
①弧AE=弧BF;②△OGH是等腰直角三角形;③四边形OGBH的面积随着点E位置的变化而变化;④△GBH周长的最小值为4+2
 .
.其中正确的是_____.(把你认为正确结论的序号都填上)

相关试题

