【题目】如图，直线l上有三个正方形a,b,c,若a,c的面积分别为5和11，则b的面积为（ ）

A. 16 B. 6 C. 55 D. 26

参考答案：

【答案】A

【解析】分析：运用正方形边长相等，再根据同角的余角相等可得∠ABC=∠DCE，然后证明△ACB≌△DCE，再结合全等三角形的性质和勾股定理来求解即可．

详解：

由于a、b、c都是正方形，所以BC=CE，∠BCE=90°；

∵∠ACB+∠ABC=∠ACB+∠DCE=90°，

即∠ABC=∠DCE，

在△ABC和△CED中，，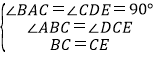

∴△ACB≌△DCE（AAS），

∴AB=CD，AC=DE；

在Rt△ABC中，由勾股定理得：BC2=AB2+AC2=AB2+DE2，

即Sb=Sa+Sc=11+5=16.

故选A．

关闭