【题目】在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 三边的长分别为
三边的长分别为![]() ,
, ![]() ,
, ![]() ,求这个三角形的面积.
,求这个三角形的面积.
小明同学在解答这道题时,先建立了一个正方形网格(每个小正方形的边长为1),再在网格中
画出格点△ABC中,(即△ABC三个顶点都在小正方形的顶点处),如图1所示,这样不需要△ABC高,借用网格就能计算出它的面积.
(1)△ABC的面积为 ;
(2)如果△MNP三边的长分别为![]() ,
, ![]() ,
, ![]() ,请利用图2的正方形网格(每个小正方形的边长为1)画出相应的格点△MNP,并直接写出△MNP的面积为 .
,请利用图2的正方形网格(每个小正方形的边长为1)画出相应的格点△MNP,并直接写出△MNP的面积为 .

参考答案:
【答案】(1)4.5;(2)作图见解析,7.
【解析】试题分析:(1)根据网格图结合割补法可得:S△ABC=S矩形MONC-S△CMA-S△AOB-S△BNC=12-2-1-4.5=4.5;(2)利用割补法可得:S△MNP=S矩形BMOA-S△BMP-S△MON-S△ANP= 15-1.5-2.5-4=7.
试题解析:
(1)
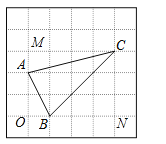
S△ABC=S矩形MONC-S△CMA-S△AOB-S△BNC=12-2-1-4.5=4.5;
(2)
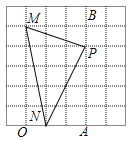
S△MNP=S矩形BMOA-S△BMP-S△MON-S△ANP= 15-1.5-2.5-4=7.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC 中,∠C=90°,BC=3,AC=4.现在要将交ABC 扩充成等腰三角形,且扩充的部分是以AC为直角边的直角三角形,求扩充后等腰三角形的周长.
赵佳同学是这样操作的:如图 1 所示,延长BC 到点 D,使CD=BC,连接AD.所以,△ADB 为符合条件的三角形.则此时△ADB的周长为____________.
请你在图2、图3中再设计两种扩充方案,并直接写出扩充后等腰三角形的周长.
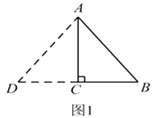
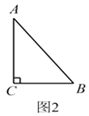
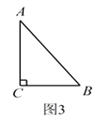
图2的周长:______________;图3的周长:______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运动属于平移的是( )
A.空中放飞的风筝
B.飞机的机身在跑道上滑行至停止
C.运动员投出的篮球
D.乒乓球比赛中高抛发球后,乒乓球的运动方式 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一张矩形纸片ABCD中,AD=4cm,点E,F分别是CD和AB的中点.现将这张纸片折叠,使点B落在EF上的点G处,折痕为AH.若HG的延长线恰好经过点D,则CD的长为( )
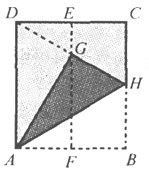
A. 2cm B.
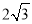 cm C. 4cm D.
cm C. 4cm D. 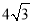 cm
cm -
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:2x﹣3=3x+4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知ABCD的顶点A、C分别在直线x=2和x=5上,O是坐标原点,则对角线OB长的最小值为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】刘卫同学在一次课外活动中,用硬纸片做了两个直角三角形,见图①、②.图①中,∠B=90°,∠A=30°,BC=6cm;图②中,∠D=90°,∠E=45°,DE=4 cm.图③是刘卫同学所做的一个实验:他将△DEF的直角边DE与△ABC的斜边AC重合在一起,并将△DEF沿AC方向移动.在移动过程中,D、E两点始终在AC边上(移动开始时点D与点A重合).
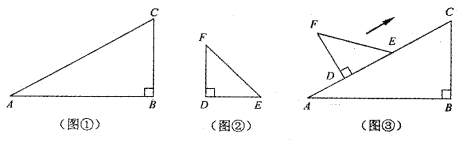
(1)在△DEF沿AC方向移动的过程中,刘卫同学发现:F、C两点间的距离逐渐 .
(2)刘卫同学经过进一步地研究,编制了如下问题:
问题①:当△DEF移动至什么位置,即AD的长为多少时,F、C的连线与AB平行?
问题②:当△DEF移动至什么位置,即AD的长为多少时,以线段AD、FC、BC的长度为三边长的三角形是直角三角形?
问题③:在△DEF的移动过程中,是否存在某个位置,使得∠FCD=15°?如果存在,
求出AD的长度;如果不存在,请说明理由.
请你分别完成上述三个问题的解答过程.
相关试题

