Question

【题目】已知二次函数y=ax2+bx-3经过A（-1,0），B（3,0）两点，

（1）求二次函数解析式及对称轴方程；

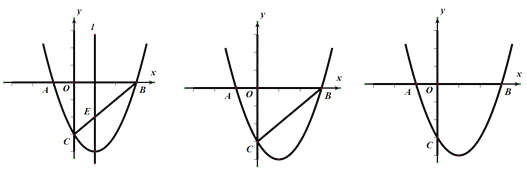
（2）连接BC，交对称轴于点E，求E点坐标；

（3）在y轴上是否存在一点M，使ΔBCM为等腰三角形，若存在，直接写出点M的坐标，若不存在，请说明理由；

（4）在第四象限内抛物线上是否存一点H，使得四边形ACHB的面积最大，若存在，求出点H坐标，若不存在，说明理由.

Answer 1

【答案】（1）二次函数解析式为y=x2-2x-3，对称轴方程为：直线x=1；

（2）E（1，-2）；

（3）存在：M1（0,3），M2（0，0），M3（0，-3-），M4（0，-3+）

（4）点H坐标为

【解析】分析：（1）将A（-1，0）、B（3，0）代入二次函数y= ，求得a、b的值即可确定二次函数的解析式；（2）求出直线BC:y=x-3, 把对称轴方程直线x=1代入，即可求解;（3）在RT△BOC中，根据勾股定理求出BC，据等腰三角形的性质求出①当BC=BM时，M1（0,3）；②当CM=BM时，点M与点O重合，M2（0，0）；③当BC=CM时，M点有两个即M3（0，-3-），M4（0，-3+）；（4）设点H的坐标为 ，连接OH，根据 .

本题解析：（1）将A，B两点坐标代入y=ax2+bx-3得方程组，解得a=1，b=-2，所以二次函数解析式为y=x2-2x-3，对称轴方程为：直线x=1；

（2）设E点坐标为(1，a),把B(3，0),C(0，-3)代入直线BC：y=kx+b,求得解析式为：y=x-3， 把x=1,代入得：a=-2, ∴E（1，-2）；

（3）存在：M1（0,3），M2（0，0），M3（0，-3-），M4（0，-3+）

（4）连接OH，设H点坐标为（x0，x02-2x0-3）

S四边形ACHB=S△AOC+S△COH+S△BOH

=+x+|x02-2x0-3|

=

=

当x0=时，x02-2x0-3=

所以点H坐标为