【题目】如图,△ABD中,∠BAD=90°,AB=AD,△ACE中,∠CAE=90°,AC=AE。
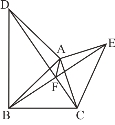
(1)求证:DC=BE;
(2)试判断∠AFD和∠AFE的大小关系,并说明理由。
参考答案:
【答案】(1)证明见解析;(2)∠AFD=∠AFE.理由见解析.
【解析】
试题分析:(1)求出∠DAC=∠BAE,根据SAS得出△DAC≌△BAE,即可得出结论;
(2)根据全等三角形的性质得出两三角形面积相等和DC=BE,根据面积公式求出AM=AN,根据角平分线的判定方法即可得出结论.
试题解析:(1)∵∠BAD=∠CAE=90°,
∴∠BAD+∠BAC=∠CAE+∠BAC,即∠DAC=∠BAE,
又AD=AB,AC=AE,
∴△DAC≌△BAE(SAS),
∴DC=BE.
(2)∠AFD=∠AFE,理由如下:
过A作AM⊥DC于M,AN⊥BE于N,如图所示:
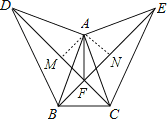
∵△DAC≌△BAE,
∴S△ACD=S△ABE,DC=BE,
∴![]() DC×AM=
DC×AM=![]() BE×AN,
BE×AN,
∴AM=AN,
∴点A在∠DFE的平分线上,
∴∠AFD=∠AFE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,是假命题的是( )
A. 同旁内角互补 B. 对顶角相等
C. 直角的补角仍然是直角 D. 两点之间线段最短
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某校八年级500名学生的体重情况,从中抽查了60名学生的体重进行统计分析,在这个问题中,总体是指( )
A. 500名学生 B. 被抽取的60名学生
C. 500名学生的体重 D. 被抽取的60名学生的体重
-
科目: 来源: 题型:
查看答案和解析>>【题目】用反证法证明“等腰三角形的底角是锐角”时首先应假设___________________.
-
科目: 来源: 题型:
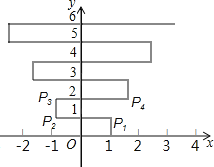
查看答案和解析>>【题目】如图,在平面直角坐标系上有个点P(1,0),点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(﹣1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,…依此规律跳动下去,P4的坐标是 ,点P第8次跳动至P8的坐标为 ;则点P第256次跳动至P256的坐标是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题:①一组对边平行,另一组对边相等的四边形是平行四边形;②对角线互相平分的四边形是平行四边形;③在四边形ABCD中,AB=AD,BC=DC,那么这个四边形ABCD是平行四边形;④一组对边相等,一组对角相等的四边形是平行四边形.其中正确的命题是_________________(将命题的序号填上即可)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果两个角的一边在同一直线上,另一边互相平行,那么这两个角只能( )
A.相等 B.互补 C.相等或互补 D.相等且互补
相关试题

