搜索
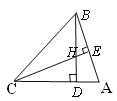
【题目】如图，在△ABC中，∠A︰∠B︰∠C=5︰4︰3，BD、CE分别是边AC、AB上的高，BD、CE相交于点H，求∠BHC的度数.
参考答案：
【答案】105°
【解析】试题分析：本题先根据三角形内角和定理，求出△ABC三个内角的度数；然后利用垂直定义及四边形AEHD的内角和等于360°，求出∠EHD的度数，即∠BHC的度数．
试题解析：解：在△ABC中，∵∠A=5x°，∠ABC=4x°，∠ACB=3x°．
又∵∠A+∠ABC+∠ACB=180°，∴5x°+4x°+3x°=180°，解得x=15，∠A=5x°=75°，∵BD，CE分别是边AC，AB上的高，∴∠ADB=90°，∠BEC=90°，∵在四边形AEHD中，∠DHE=360°﹣∠ADB﹣∠AEC﹣∠A=360°﹣90°﹣90°﹣75°=105°，∴∠BHC=∠DHE =105°．
-
科目： 来源： 题型：
查看答案和解析>>【题目】若定义：f（a，b）=（﹣a，b），g（m，n）=（m，﹣n），例如f（1，2）=（﹣1，2），g（﹣4，﹣5）=（﹣4，5），则g（f（2，﹣3））=（ ）
A.（2，﹣3）
B.（﹣2，3）
C.（2，3）
D.（﹣2，﹣3） -
科目： 来源： 题型：
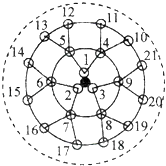
查看答案和解析>>【题目】生物课题研究小组对附着在物体表面的三个微生物（课题组成员把他们分别标号为1，2，3）的生长情况进行观察记录，这三个微生物第一天各自一分为二，产生新的微生物（依次被标号为4，5，6，7，8，9），接下去每天都按照这样的规律变化，即每个微生物一分为二，形成新的微生物（课题组成员用如图所示的图形进行形象的记录），那么标号为1000的微生物会出现在（ ）
A.第7天
B.第8天
C.第9天
D.第10天 -
科目： 来源： 题型：
查看答案和解析>>【题目】一元一次方程2x+1=3的解是x=_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】(1)计算：(x＋3y)2＋(2x＋y)(x-y)；
(2)计算：
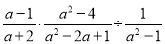
(3)分解因式：x3-2x2y＋xy2.
(4)解方程：
-
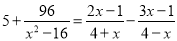
科目： 来源： 题型：
查看答案和解析>>【题目】中国的国土面积约为9600000平方千米，用科学记数法表示为（ ）
A. 96×105 B. 0.96×107 C. 9.6×106 D. 9.6×107
-
科目： 来源： 题型：
查看答案和解析>>【题目】正方形ABCD边长为4，M、N分别是BC、CD上的两个动点，当M点在BC上运动时，保持AM和MN垂直，
（1）证明：Rt△ABM ∽Rt△MCN；
（2）设BM=x，梯形ABCN的面积为y，求y与x之间的函数关系式；当M点运动到什么位置时，四边形ABCN的面积最大，并求出最大面积；
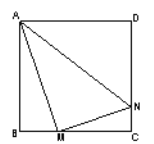（3）当M点运动到什么位置时Rt△ABM∽Rt△AMN，求此时x的值.
相关试题
