Question

【题目】某公司专销产品A，第一批产品A上市40天内全部售完、该公司对第一批产品A上市后的市场销售情况进行了跟踪调查，调查结果如图所示，其中图（1）中的折线表示的是市场日销售量与上市时间的关系；图（2）中的折线表示的是每件产品A的销售利润与上市时间的关系．

（1）写出第一批产品A的市场日销售量y与上市时间t的关系式；

（2）写出每件产品A的销售利润y与上市时间t的关系式；

（3）第一批产品A上市后，哪一天这家公司市场日销售利润最大？最大利润是多少万元？

Answer 1

【答案】(1) y=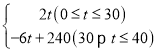；(2) y=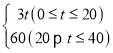；(3)第30天时，日销售利润最大，最大利润是3600万元．

【解析】

试题分析：（1）根据0≤t≤30、30＜t≤40两种情况，利用待定系数法分别求解可得；

（2）分0≤t≤20、20＜t≤40两种情况，分别求解可得；

（3）分0≤t≤20、20＜t≤30、30＜t≤40三种情况，根据总利润=每件产品利润×日销售量，分别求出其最大值，比较后即可得．

试题解析：（1）由图1可得，

当0≤t≤30时，设市场的日销售量y=kt，

∵点（30，60）在图象上，∴60=30k，

∴k=2，即y=2t；

当30＜t≤40时，设市场的日销售量y=t+b，

∵点（30，60）和（40，0）在图象上，

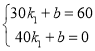∴，解得，

∴y=﹣6t+240．

故y=；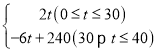

（2）由图②可得：

当0≤t≤20时，每件产品的日销售利润为y=3t；

当20＜t≤40时，每件产品的日销售利润为y=60；

故y=；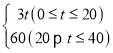

（3）①当0≤t≤20时，

y=3t×2t=，

t=20时，y的最大值为2400（万元）；

②当20＜t≤30时，

y=2t×60=120t，

t=30时，y的最大值为3600（万元）；

③当30＜t≤40时，

y=60（﹣6t+240）=﹣360t+14400，

∵k=﹣360＜0，

∴y随t的增大而减小．

∴y＜﹣360×30+14400

即y＜3600（万元）

∴第30天时，日销售利润最大，最大利润是3600万元．